题目内容
【题目】如图,在5×5的正方形网格中,从在格点上的点A,B,C,D中任取三点,所构成的三角形恰好是直角三角形的个数为( )
A.1
B.2
C.3
D.4
【答案】C
【解析】解:
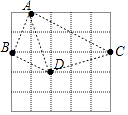
理由是:连接AC、AB、AD、BC、CD、BD,
设小正方形的边长为1,
由勾股定理得:AB2=12+22=5,AC2=22+42=20,AD2=12+32=10,BC2=52=25,CD2=12+32=10,BD2=12+22=5,
∴AB2+AC2=BC2,AD2+CD2=AC2,BD2+AB2=AD2,
∴△ABC、△ADC、△ABD是直角三角形,共3个直角三角形,
所以答案是:C.
【考点精析】利用勾股定理的概念和勾股定理的逆定理对题目进行判断即可得到答案,需要熟知直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;如果三角形的三边长a、b、c有下面关系:a2+b2=c2,那么这个三角形是直角三角形.

练习册系列答案
相关题目
【题目】下表中有两种移动电话计费方式:
月使用费(元) | 主叫限定时间(分钟) | 主叫超时费(元/分钟) | 被叫 | |
方式一 | 65 | 160 | 0.25 | 免费 |
方式二 | 100 | 380 | 0.19 | 免费 |
说明:月使用费固定收取,主叫不超限定时间不再收费,主叫超时部分加收超时费;被叫免费.
(1)若李杰某月主叫通话时间为200分钟则他按方式一计费需 元,按方式二计费需 元;若他按方式二计费需103.8元,则主叫通话时间为 分钟;
(2)是否存在某主叫通话时间t(分钟),按方式一和方式二的计费相等,若存在,请求出t的值;若不存在,请说明理由;
(3)请你通过计算分析后,直接给出当月主叫通话时间t(分钟)满足什么条件时,选择方式一省钱;当每月主叫通话时间t(分钟)满足什么条件时,选择方式二省钱.