题目内容
【题目】定义:我们知道,四边形的一条对角线把这个四边形分成了两个三角形,如果这两个三角形相似(不全等),我们就把这条对角线叫做这个四边形的“相似对角线”;
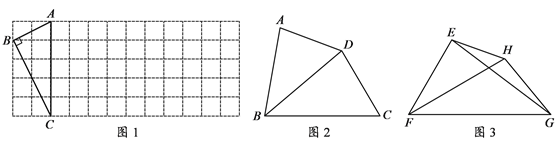
理解:
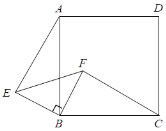
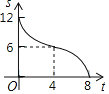
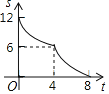
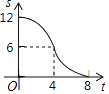
⑴ 如图1,△ABC的三个顶点均在正方形网格中的格点上,若四边形ABCD是以AC为“相似对角线”的四边形,请用无刻度的直尺在网格中画出点D(保留画图痕迹,找出3个即可);
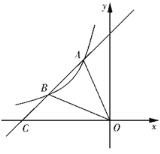
⑵ 如图2,在四边形ABCD中,∠ABC=80°,∠ADC=140°,对角线BD平分∠ABC. 请问BD是四边形ABCD的“相似对角线”吗?请说明理由;
运用:
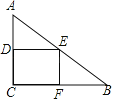
⑶ 如图3,已知FH是四边形EFGH的“相似对角线”, ∠EFH=∠HFG=30°.连接EG,若△EFG的面积为![]() ,求FH 的长.
,求FH 的长.
【答案】(1)如图1,△ACD1、△ACD2、、△ACD3、△ACD4(任画三个即可);(2)BD是四边形ABCD的“相似对角线”,理由见解析;(3)FH=![]() .
.
【解析】
(1)根据“相似对角线”的定义,利用方格纸的特点可找到D点的位置;
(2)先说明∠A+∠ADB=140°=∠ADC,即可说明理由;
(3)先判断出△FEHC∽△FHG,得出FH2=FE·FG,再求出EQ=![]() FE,即可求得FH的值.
FE,即可求得FH的值.
解:(1)由图1可得,AB=![]() ,BC=2
,BC=2![]() ,∠ABC=90°,AC=5,
,∠ABC=90°,AC=5,
四边形ABCD是以AC为“相似对角线”的四边形,
①当∠ACD=90°时,△ACD∽△ABC或△ACD∽△CBA,
∴![]() 或
或![]()
∴CD=10或CD=2.5
同理:当∠CAD=90°时,AD=2.5或AD=10.
根据方格纸的特点可找到D点的位置,然后再连接CD或AD
即如图△ACD1、△ACD2、、△ACD3、△ACD4(任画三个即可)即为所求;
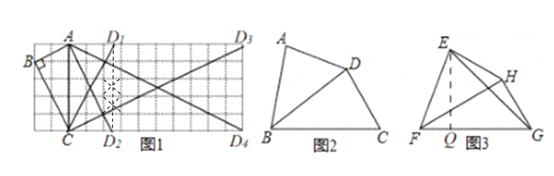
(2)BD是四边形ABCD的“相似对角线”,理由如下:
∵∠ABC=80°,BD平分∠ABC,
∴∠ABD=∠DBC=40°,
∵∠A+∠ADB=140°
∵∠ADC=140°,
∴∠BDC+∠ADB=140°,
∴∠A=∠BDC,
∴△ABD∽△DBC,
∴BD是四边形ABCD的“相似对角线”;
(3)∵FH是四边形EFGH的“相似对角线”,
∴△EFH与△HFG相似,
∵∠EFH=∠HFG,
∴△FEHC∽△FHG,
∴![]()
∴FH2=FE·FG,
如图3,过点E作EQ⊥FG于Q,
∴EQ=FE·sin60°=![]() FE,
FE,
∵![]() .
.
∴![]()
∴FG·FE=24,
∵FH2=FE·FG,
∴FH2=24
∴FH=![]() ,FH=-
,FH=-![]() (舍去)
(舍去)

 阅读快车系列答案
阅读快车系列答案