题目内容
14、如图，O是边长为6的等边三角形ABC内的任意一点，且OD∥BC，交AB于点D，OF∥AB，交AC于F，OE∥AC，交BC于E．则OD+OE+OF的值（ ）分析：根据等边三角形，平行线的性质，和平行四边形的判定，并根据等腰梯形性质求解．
解答：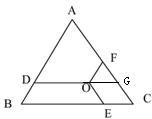
解：延长OD交AC于点G，
∵OE∥CG，OG∥CE，∴四边形OGCE是平行四边形，有OE=CG，∠OGF=∠C=60°，∵OF∥AB，∴∠OFG=∠A=60°，∴OF=OG，∴△OGF是等边三角形，∴OF=FG，∵OD∥BC，∴∠ADO=∠B=60°
∴梯形OFAD是等腰梯形，有OD=AF，即OD+OE+OF=AF+FG+CG=AC=6．
故选D．
解：延长OD交AC于点G，∵OE∥CG，OG∥CE，∴四边形OGCE是平行四边形，有OE=CG，∠OGF=∠C=60°，∵OF∥AB，∴∠OFG=∠A=60°，∴OF=OG，∴△OGF是等边三角形，∴OF=FG，∵OD∥BC，∴∠ADO=∠B=60°
∴梯形OFAD是等腰梯形，有OD=AF，即OD+OE+OF=AF+FG+CG=AC=6．
故选D．
点评：本题利用了：
1、等腰三角形的性质和判定：三边相等，三角均为60度，有两角相等且为60度的三角形是等边三角形；
2、平行四边形的判定的性质；
3、等腰梯形的判定和性质．
1、等腰三角形的性质和判定：三边相等，三角均为60度，有两角相等且为60度的三角形是等边三角形；
2、平行四边形的判定的性质；
3、等腰梯形的判定和性质．
练习册系列答案
阅读快车系列答案
相关题目
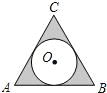如图，⊙O是边长为2的等边三角形ABC的内切圆，则图中阴影部分的面积为
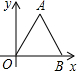如图，△AOB是边长为5的等边三角形，则A，B两点的坐标分别是A
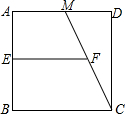如图，M是边长为2cm的正方形ABCD的边AD的中点，E、F分别是AB、CM的中点．则EF=
如图，△ABC是边长为6的等边三角形，AD=2，AE∥BC，直线BD交AE于点E，则BE的长为（ ）