Question

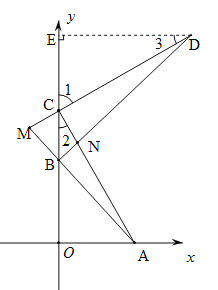
【题目】如图，在平面直角坐标系中，OA=OB，AC=CD，已知两点A(4，0)，C(0，7)，点D在第一象限内，∠DCA=90°，点B在线段OC上，AB的延长线与DC的延长线交于点M，AC与BD交于点N.

（1）点B的坐标为：　 　；

（2）求点D的坐标；

（3）求证：CM=CN.

Answer 1

【答案】（1）（0，4）；（2）D（7,11）；（3）证明见解析.

【解析】

（1）由A(4，0)和OA=OB即可得到结论；

（2）过点D作DE⊥y轴，垂足为E，证明△DEC≌△COA，即可得到结论；

（3）证明△DBE是等腰直角三角形，得到∠DBE=45°，从而得到∠DBA=90°.在△DNC和△ABN中，根据三角形内角和定理可得出∠CDN=∠BAN，从而证明△DCN≌△ACM，根据全等三角形对应边相等即可得出结论.

（1）∵A(4，0)，

∴OA=OB=4，

∴B(0，4)；

（2）∵C(0，7)，

∴OC=7.

过点D作DE⊥y轴，垂足为E，

∴∠DEC=∠AOC=90°.

∵∠DCA=90°，

∴∠1+∠2=∠1+∠3=90°，

∴∠2=∠3，

∴△DEC≌△COA(AAS)，

∴DE=OC=7，EC=OA=4，

∴OE=OC+EC=11，

∴D(7，11).

（3）∵BE=OE-OB=11-4=7，

∴BE=DE，

∴△DBE是等腰直角三角形，

∴∠DBE=45°.

∵OA=OB，

∴∠OBA=45°，

∴∠DBA=90°，

∴∠BAN+∠ANB=90°.

∵∠DCA=90°，

∴∠CDN+∠DNC=90°.

∵∠DNC=∠ANB，

∴∠CDN=∠BAN.

∵∠DCA=90°，

∴∠ACM=∠DCN=90°，

∴△DCN≌△ACM(ASA)，

∴CM=CN.