题目内容
【题目】为了测量学校旗杆的高度,身高相同的小张和小李站在操场如图所示的位置,小张在C处测得旗杆顶端的仰角为18°,小李在D处测得旗杆顶端的仰角为72°,又已知两人之间的距离CD为24米,两人的眼睛离地面的距离AC、BD均为1.6米,旗杆的底部N距离操场所在平面的垂直高度NK=2米,求旗杆MN的高度.(参考数据:tan18°≈![]() .)
.)
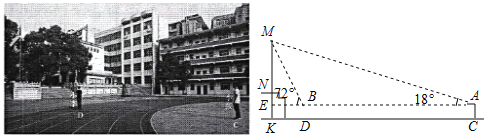
【答案】旗杆MN的高度是8.6米.
【解析】试题分析:设ME=x,通过解直角△EBM得到ME的长度,通过解直角△AME得到ME的长度,由此列出方程求得x的值,然后结合图形找到相关线段的和差关系进行解答.
试题解析:设ME=x.
∵在直角△AME中,∠MAE=18°,
∴EM=AEtan18°=![]() AE.即AE=3x;
AE.即AE=3x;
∵在直角△EBM中,∠MBE=72°,
∴ME=BEtan72°=3BE,即BE=![]() ME,
ME,
∴3x-![]() x=24,
x=24,
解得x=9,
∴MK=10.6米,
又NK=2米,
∴MN=10.6-2=8.6(米).
答:旗杆MN的高度是8.6米.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
【题目】甲、乙两位同学参加数学综合素质测试,各项成绩如下(单位:分)
数与代数 | 空间与图形 | 统计与概率 | 综合与实践 | |
学生甲 | 90 | 93 | 89 | 90 |
学生乙 | 94 | 92 | 94 | 86 |
(1)分别计算甲、乙成绩的中位数;
(2)如果数与代数、空间与图形、统计与概率、综合与实践的成绩按3:3:2:2计算,那么甲、乙的数学综合素质成绩分别为多少分?