题目内容
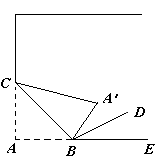
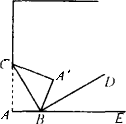
 如图,将书角折过去,该角顶点C落在E处,GF为折痕,FH为∠EFB的角平分线,则∠GFH=________度.
如图,将书角折过去,该角顶点C落在E处,GF为折痕,FH为∠EFB的角平分线,则∠GFH=________度.
90
分析:根据折叠的性质得到∠GFC=∠GFE,再由角平分线的性质得到∠EFH=∠HFB,而∠GFC+∠GFE+∠EFH+∠HFB=180°,即可得到∠GFH=90°.
解答:∵把书面斜折过去,使顶点C落在E处,FG为折痕,
∴∠GFC=∠GFE,
而FH为∠EFB的平分线,
∴∠EFH=∠HFB,
∠GFC+∠GFE+∠EFH+∠HFB=180°,
∴∠GFE+∠EFH=90°,
即∠GFH=90°.
故答案为:90.
点评:本题考查了折叠的性质及角的计算:折叠前后两图形全等,即得到对应角相等,对应线段相等.也考查了角平分线的性质.
分析:根据折叠的性质得到∠GFC=∠GFE,再由角平分线的性质得到∠EFH=∠HFB,而∠GFC+∠GFE+∠EFH+∠HFB=180°,即可得到∠GFH=90°.
解答:∵把书面斜折过去,使顶点C落在E处,FG为折痕,
∴∠GFC=∠GFE,
而FH为∠EFB的平分线,
∴∠EFH=∠HFB,
∠GFC+∠GFE+∠EFH+∠HFB=180°,
∴∠GFE+∠EFH=90°,
即∠GFH=90°.
故答案为:90.
点评:本题考查了折叠的性质及角的计算:折叠前后两图形全等,即得到对应角相等,对应线段相等.也考查了角平分线的性质.

练习册系列答案
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案
相关题目
 如图,将书角折过去,该角顶点C落在E处,GF为折痕,FH为∠EFB的角平分线,则∠GFH=
如图,将书角折过去,该角顶点C落在E处,GF为折痕,FH为∠EFB的角平分线,则∠GFH=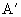 处,BC为折痕,且
处,BC为折痕,且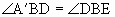 ,则∠CBD=________度.
,则∠CBD=________度.