题目内容
 已知:在等腰梯形ABCD中,AD∥BC,AB=CD=5,EF是梯形ABCD的中位线,且EF=6,则梯形ABCD的周长是
已知:在等腰梯形ABCD中,AD∥BC,AB=CD=5,EF是梯形ABCD的中位线,且EF=6,则梯形ABCD的周长是
- A.24
- B.22
- C.20
- D.16
B
分析:根据梯形的中位线定理:中位线= (上底+下底),求得上底AD与下底BC的和;然后根据已知条件“AB=CD=5、EF=6”、梯形的周长的定义(梯形的边长之和)来求梯形的周长即可.
(上底+下底),求得上底AD与下底BC的和;然后根据已知条件“AB=CD=5、EF=6”、梯形的周长的定义(梯形的边长之和)来求梯形的周长即可.
解答:设梯形ABCD的周长是l.
∵EF是梯形ABCD的中位线,
∴EF= (AD+BC);
(AD+BC);
又∵AB=CD=5,l=AB+CD+AD+BC,EF=6,
∴l=2(AB+AE)=22;
故选B.
点评:本题考查了梯形的中位线定理和等腰梯形的性质.梯形的中位线平行于两底,并且等于两底和的一半.
分析:根据梯形的中位线定理:中位线=
 (上底+下底),求得上底AD与下底BC的和;然后根据已知条件“AB=CD=5、EF=6”、梯形的周长的定义(梯形的边长之和)来求梯形的周长即可.
(上底+下底),求得上底AD与下底BC的和;然后根据已知条件“AB=CD=5、EF=6”、梯形的周长的定义(梯形的边长之和)来求梯形的周长即可.解答:设梯形ABCD的周长是l.
∵EF是梯形ABCD的中位线,
∴EF=
 (AD+BC);
(AD+BC);又∵AB=CD=5,l=AB+CD+AD+BC,EF=6,
∴l=2(AB+AE)=22;
故选B.
点评:本题考查了梯形的中位线定理和等腰梯形的性质.梯形的中位线平行于两底,并且等于两底和的一半.

练习册系列答案
相关题目
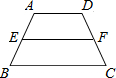 已知:在等腰梯形ABCD中,AD∥BC,AB=CD=5,EF是梯形ABCD的中位线,且EF=6,则梯形ABCD的周长是( )
已知:在等腰梯形ABCD中,AD∥BC,AB=CD=5,EF是梯形ABCD的中位线,且EF=6,则梯形ABCD的周长是( )| A、24 | B、22 | C、20 | D、16 |
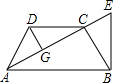 如图,已知:在等腰梯形ABCD中,AB∥CD,AC⊥BC,DG⊥AC,过B作EB⊥AB,交AC的延长线于E.
如图,已知:在等腰梯形ABCD中,AB∥CD,AC⊥BC,DG⊥AC,过B作EB⊥AB,交AC的延长线于E.
 4、已知:在等腰梯形ABCD中,AD∥BC,AB=CD=4,MN是梯形ABCD的中位线,且MN=6,则梯形ABCD的周长是( )
4、已知:在等腰梯形ABCD中,AD∥BC,AB=CD=4,MN是梯形ABCD的中位线,且MN=6,则梯形ABCD的周长是( )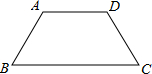 (2009•雅安)已知,在等腰梯形ABCD中,AD∥BC,AD=AB=2,∠B=60°,则梯形ABCD的周长( )
(2009•雅安)已知,在等腰梯形ABCD中,AD∥BC,AD=AB=2,∠B=60°,则梯形ABCD的周长( )