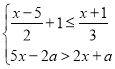题目内容
【题目】把一个自然数所有数位上的数字先平方再求和得到一个新数，叫做第一次运算，再把所得新数所有数位上的数字先平方再求和又将得到一个新数，叫做第二次运算，……如此重复下去，若最终结果为1，我们把具有这种特征的自然数称为“快乐数”．例如：
，
，
所以32和70都是“快乐数”．
（1）写出最小的两位“快乐数”；判断19是不是“快乐数”；并说明理由；
（2）若一个三位“快乐数”经过两次运算后结果为1，把这个三位“快乐数”与它的各位上的数字相加所得的和被8除余数是2，求出这个“快乐数”．
【答案】（1）10，是，理由见详解；（2）310和860.
【解析】
（1）根据“快乐数”的定义计算即可；
（2）设三位“快乐数”为100a+10b+c，根据“快乐数”的定义计算．
解：（1）∵12+02=1，
∴最小的两位“快乐数”10，
∵19→12+92=82→82+22=68→62+82=100→12+02+02=1，
∴19是快乐数；
（2）设三位“快乐数”为100a+10b+c，由题意，经过两次运算后结果为1，所以第一次运算后结果一定是10或者100，
则a2+b2+c2=10或100，
∵a、b、c为整数，且a≠0，
∴当a2+b2+c2=10时，12+32+02=10，
①a=1，b=3或0，c=0或3时，三位“快乐数”为130，103，
②当a=2时，无解；
③当a=3，b=1或0，c=0或1时，三位“快乐数”为310，301，
同理当a2+b2+c2=100时，62+82+02=100，
∴三位“快乐数”有680，608，806，860．
综上一共有130，103，310，301，680，608，806，860八个，
又因为三位“快乐数”与它的各位上的数字相加所得的和被8除余数是2，
∴只有310和860满足已知条件．
