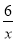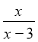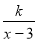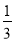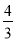Question

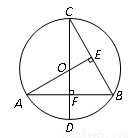
如图，CD为⊙O的直径，CD⊥AB，垂足为点F，AO⊥BC，垂足为点E，BC=.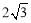

（1）求AB的长；

（2）求⊙O的半径．

 

 

Answer 1

（1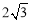）；（2）2.

【解析】

试题分析：（1）由△COE≌△AOF，根据全等三角形的性质和垂径定理即可求得结果.

（2）应用锐角三角函数定义可求得∠A有度数，从而即可求得圆O的半径AO.

（1）∵CD⊥AB，AO⊥BC， ∴∠AFO =∠CEO=90°.

∵∠COE=∠AOF，CO=AO ，∴△COE≌△AOF ．∴CE=AF.

∵CD过圆心O，且CD⊥AB， ∴AB=2AF.

同理可得： BC=2CE.

∴AB=BC=.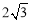

（2）在Rt△AEB中，由（1）知：AB=BC=2BE，∠AEB=90°，∴∠A=30°．

又在Rt△AOF中，∠AFO=90°，AF=， ∴.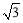

∴圆O的半径为2．

考点：1.全等三角形的判定和性质；2.垂径定理；3．锐角三角函数定义；4.特殊角的三角函数值.