题目内容
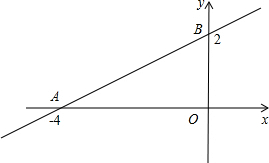 如图,直线y=
如图,直线y=| 1 | 2 |
(1)直线AB关于y轴对称的直线解析式为
(2)直线AB绕原点旋转180度后的直线解析式为
(3)将直线AB绕点P(-1,0)顺时针方向旋转90度,求旋转后的直线解析式.
分析:(1)先根据关于y轴对称确定两个坐标,然后运用待定系数法求解;
(2)根据关于原点对称的两点的横坐标纵坐标都互为相反数求确定两个点的坐标,然后利用待定系数法求解;
(3)旋转90°所得的直线的k与原直线的k互为负倒数,再根据点(-1,3)可得出答案.
(2)根据关于原点对称的两点的横坐标纵坐标都互为相反数求确定两个点的坐标,然后利用待定系数法求解;
(3)旋转90°所得的直线的k与原直线的k互为负倒数,再根据点(-1,3)可得出答案.
解答:解:由题意得:A(-4,0),B(0,2),
(1)∵关于y轴对称则:此直线过点(0,2)和(4,0),
∴可得函数解析式为i:y=-
x+2;
(2)∵关于原点对称的两点的横坐标纵坐标都互为相反数,
∴可得函数解析式过点(0,-2)和(4,0),
∴函数解析式为:y=
x-2
(3)设函数解析式为y=-2x+b,
又∵过点(-1,3),
∴函数解析式为:y=-2x+1.
故答案为:y=-
x+2;y=
x-2.
(1)∵关于y轴对称则:此直线过点(0,2)和(4,0),
∴可得函数解析式为i:y=-
| 1 |
| 2 |
(2)∵关于原点对称的两点的横坐标纵坐标都互为相反数,
∴可得函数解析式过点(0,-2)和(4,0),
∴函数解析式为:y=
| 1 |
| 2 |
(3)设函数解析式为y=-2x+b,
又∵过点(-1,3),
∴函数解析式为:y=-2x+1.
故答案为:y=-
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题考查待定系数法求函数解析式,难度不大,关键是掌握几种对称的特点.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,直线y=-
如图,直线y=- D为直径作⊙A交CD于F,FA的延长线交⊙A于E,交x轴于B.
D为直径作⊙A交CD于F,FA的延长线交⊙A于E,交x轴于B. 如图,直线y=-
如图,直线y=- (2013•蒙山县一模)如图,直线
(2013•蒙山县一模)如图,直线