题目内容
在直角坐标系中,O为坐标原点,已知A(1,1),在x轴上确定点P,使△AOP为等腰三角形,则符合条件的点P的个数共有________个,点P的坐标分别为________.
4 (2,0),(1,0),( ,0),(-
,0),(- ,0)
,0)
分析:有三种情况:当OA=OP时,以O为圆心,以OA为半径画弧交X轴于两点,根据勾股定理求出OP即可;当OA=AP时,以A为圆心,以OA为半径画弧交X轴于一点,求出OP即可;当OP=AP时,过A作PA⊥X轴于P,即可得到P的坐标.
解答:当OA=OP时,以O为圆心,以OA为半径画弧交X轴于两点,根据勾股定理求出OP=OA= ,
,
∴P( ,0),P(-
,0),P(- ,0);
,0);
当OA=AP时,以A为圆心,以OA为半径画弧交X轴于一点,则OP=1+1=2,
∴P(2,0);
当OP=AP时,过A作PA⊥X轴于P,
∴P(1,0),
故答案为:4,(2,0),(1,0),( ,0),(-
,0),(- ,0).
,0).
点评:本题主要考查对等腰三角形的性质,坐标与图形的性质等知识点的理解和掌握,能正确进行分类求出所有的情况是解此题的关键.
 ,0),(-
,0),(- ,0)
,0)分析:有三种情况:当OA=OP时,以O为圆心,以OA为半径画弧交X轴于两点,根据勾股定理求出OP即可;当OA=AP时,以A为圆心,以OA为半径画弧交X轴于一点,求出OP即可;当OP=AP时,过A作PA⊥X轴于P,即可得到P的坐标.
解答:当OA=OP时,以O为圆心,以OA为半径画弧交X轴于两点,根据勾股定理求出OP=OA=
 ,
,∴P(
 ,0),P(-
,0),P(- ,0);
,0);当OA=AP时,以A为圆心,以OA为半径画弧交X轴于一点,则OP=1+1=2,
∴P(2,0);
当OP=AP时,过A作PA⊥X轴于P,
∴P(1,0),
故答案为:4,(2,0),(1,0),(
 ,0),(-
,0),(- ,0).
,0).点评:本题主要考查对等腰三角形的性质,坐标与图形的性质等知识点的理解和掌握,能正确进行分类求出所有的情况是解此题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
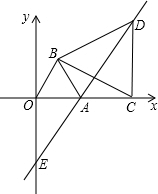 OAB,C为x轴正半轴上的一个动点(OC>1),连接BC,以BC为边在第一象限内作等边△BCD,直线DA交y轴于E点.
OAB,C为x轴正半轴上的一个动点(OC>1),连接BC,以BC为边在第一象限内作等边△BCD,直线DA交y轴于E点.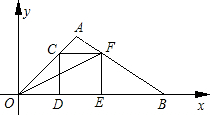 在直角坐标系中,O为坐标原点,点A的坐标为(2,2),点C是线段OA上的一个动点(不运动至O,A两点),过点C作CD⊥x轴,垂足为D,以CD为边在右侧作正方形CDEF.连接AF并延长交x轴的正半轴于点B,连接OF,设OD=t.
在直角坐标系中,O为坐标原点,点A的坐标为(2,2),点C是线段OA上的一个动点(不运动至O,A两点),过点C作CD⊥x轴,垂足为D,以CD为边在右侧作正方形CDEF.连接AF并延长交x轴的正半轴于点B,连接OF,设OD=t.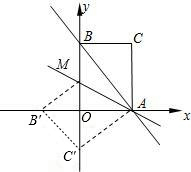 点B′处,C的对应点为C′.
点B′处,C的对应点为C′.