Question

【题目】在 Rt 中，， ，点 为射线 上一点，连接 ，过点 作线段 的垂线 ，在直线 上，分别在点 的两侧截取与线段 相等的线段 和 ，连接 ，．

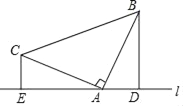
（1）当点 在线段 上时（点 不与点 ， 重合），如图1，

①请你将图形补充完整；

②线段 ， 所在直线的位置关系为 ，线段 ， 的数量关系为/span> ；

（2）当点 在线段 的延长线上时，如图2，

①请你将图形补充完整；

②在（1）中②问的结论是否仍然成立?如果成立请进行证明，如果不成立，请说明理由．

Answer 1

【答案】（1）①见详解，②垂直、相等；（2）①见详解，②成立，理由见详解

【解析】

（1）①D在线段AB上时，在直线l上截取CE=CF=CD，即可画出图象．②在图1中证明△ACD≌△BCF得到AD=BF，∠BAC=∠FBC，利用∠ABF=∠ABC+∠FBC=∠ABC+∠BAC=90°，即BF⊥AD．
（2）①D在线段AB延长线上时，在直线l上截取CE=CF=CD，即可画出图象．②在图2中证明△ACD≌△BCF得到AD=BF，∠BAC=∠FBC，利用∠ABF=∠ABC+∠FBC=∠ABC+∠BAC=90°，即BF⊥AD．

解：（1）①见图1所示．

②证明：∵CD⊥EF，
∴∠DCF=90°，
∵∠ACB=90°，
∴∠ACB=∠DCF，
∴∠ACD=∠BCF
∵BC=AC，CD=CF，
∴△ACD≌△BCF，
∴AD=BF，∠BAC=∠FBC，
∴∠ABF=∠ABC+∠FBC=∠ABC+∠BAC=90°，
即BF⊥AD．
故答案为：垂直、相等．

（2）①见图2所示．

②成立．理由如下：
证明：∵CD⊥EF，
∴∠DCF=90°，
∵∠ACB=90°，
∴∠DCF+∠BCD=∠ACB+∠BCD，
即∠ACD=∠BCF，
∵BC=AC，CD=CF，
∴△ACD≌△BCF，
∴AD=BF，∠BAC=∠FBC，
∴∠ABF=∠ABC+∠FBC=∠ABC+∠BAC=90°，
即BF⊥AD．