题目内容
已知:如图1,△OAB是边长为2的等边三角形,OA在x轴上,点B在第一象限内;△OCA是一个等腰三角形,OC=AC,顶点C在第四象限,∠C=120°.现有两动点P、Q分别从A、O两点同时出发,点Q以每秒1个单位的速度沿OC向点C运动,点P以每秒3个单位的速度沿A→O→B运动,当其中一个点到达终点时,另一个点也随即停止.

(1)求在运动过程中形成的△OPQ面积S与运动时间t之间的函数关系,并写出自变量t的取值范围;
(2)在OA上(点O、A除外)存在点D,使得△OCD为等腰三角形,请直接写出所有符合条件的点D的坐标;
(3)如图2,现有∠MCN=60°,其两边分别与OB、AB交于点M、N,连接MN.将∠MCN绕着C点旋转(0°<旋转角<60°),使得M、N始终在边OB和边AB上.试判断在这一过程中,△BMN的周长是否发生变化?若没有变化,请求出其周长;若发生变化,请说明理由.

(1)求在运动过程中形成的△OPQ面积S与运动时间t之间的函数关系,并写出自变量t的取值范围;
(2)在OA上(点O、A除外)存在点D,使得△OCD为等腰三角形,请直接写出所有符合条件的点D的坐标;
(3)如图2,现有∠MCN=60°,其两边分别与OB、AB交于点M、N,连接MN.将∠MCN绕着C点旋转(0°<旋转角<60°),使得M、N始终在边OB和边AB上.试判断在这一过程中,△BMN的周长是否发生变化?若没有变化,请求出其周长;若发生变化,请说明理由.

(1) (
(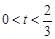 ),
),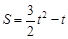 (
(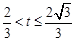 )
)
(2)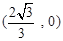 或
或
(3)4
 (
(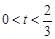 ),
),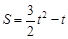 (
(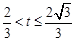 )
)(2)
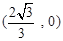 或
或
(3)4
试题分析:解:(1)过点C作CD⊥OA于点D.
∵OC=AC,∠ACO=120°,∴∠AOC=∠OAC=30°.
∵
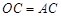 ,
,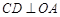 , ∴
, ∴ .
. 在Rt
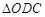 中,
中,
①当
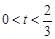 时,
时,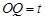 ,
,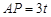 ,
,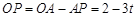 ;
;过点
 作
作 于点
于点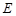 .
.在Rt
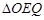 中,∵
中,∵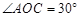 ,∴
,∴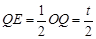 ,
,∴
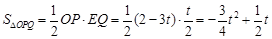 .
.即
 .
. ②当
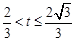 时,
时,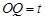 ,
,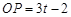 .
.∵
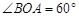 ,
,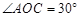 ,∴
,∴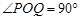 .
.∴
 .
.即
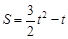 .
.故当
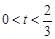 时,
时, ,当
,当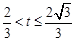 时,
时,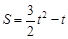
(2)因为点C(1,-
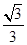 ),所以OC=
),所以OC= ,假设OC=OD,则点D的坐标为
,假设OC=OD,则点D的坐标为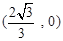
假设OD=DC,则点D的坐标为

(3)
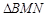 的周长不发生变化.
的周长不发生变化.延长
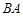 至点
至点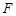 ,使
,使 ,连结
,连结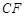 .
.∵
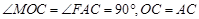 ,∴
,∴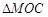 ≌
≌ .
.∴
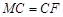 ,
,
∴
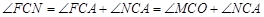
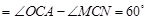 .
.∴
 . 又∵
. 又∵ .
.∴
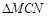 ≌
≌ .∴
.∴
∴

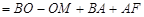
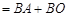
 .
.∴
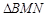 的周长不变,其周长为4
的周长不变,其周长为4点评:该题较为复杂,是大题中的常考题,主要考查学生分析直角坐标系几何图形与函数之间的联系,图形点的坐标表示记得所在空间的符号。

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 的图象交于A(1,4)B(4,n)两点,与
的图象交于A(1,4)B(4,n)两点,与 轴交于D点,AC⊥
轴交于D点,AC⊥
 (x<0)的图象相交于A点,与y轴、x轴分别相交于B、C两点,且C(2,0),A点的横坐标为-1.
(x<0)的图象相交于A点,与y轴、x轴分别相交于B、C两点,且C(2,0),A点的横坐标为-1.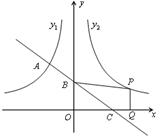
 (x>0)的图象与
(x>0)的图象与 (x<0)的图象关于y轴对称,在
(x<0)的图象关于y轴对称,在 ,点E是AD的三等分点,且AE
,点E是AD的三等分点,且AE DE,过点E作EF∥AB交BC于F,并作射线DC和AB,点P、Q分别是射线DC和射线AB上动点,点P以每秒1个单位的速度向右平移,且始终满足∠PQA=60°,设P点运动的时间为
DE,过点E作EF∥AB交BC于F,并作射线DC和AB,点P、Q分别是射线DC和射线AB上动点,点P以每秒1个单位的速度向右平移,且始终满足∠PQA=60°,设P点运动的时间为 .
.
 为等腰三角形?若存在,请直接写出时间
为等腰三角形?若存在,请直接写出时间 与四边形
与四边形 的重叠部分的面积为S,试求S与
的重叠部分的面积为S,试求S与 与x轴、y轴分别交于A、B两点,点M是OB上一点,若直线AB沿AM折叠,点B恰好落在x轴上的点C处,则点M的坐标是
与x轴、y轴分别交于A、B两点,点M是OB上一点,若直线AB沿AM折叠,点B恰好落在x轴上的点C处,则点M的坐标是
 的图象与
的图象与 轴的交点在
轴的交点在 轴的上方,则
轴的上方,则 的取值范围为 .
的取值范围为 .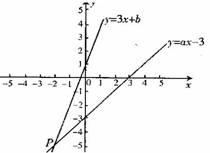
 是正比例函数,则a=___________。
是正比例函数,则a=___________。