Question

为了从甲、乙两名选手中选拔一个参加射击比赛，现对他们进行一次测验，两人在相同条件下各射靶10次，为了比较两人的成绩，制作了如下统计图表： (1)请补全上述图表(请直接在表中填空和补全折线图)； (2)如果规定成绩较稳定者胜出，你认为谁应胜出？说明你的理由； (3)如果希望(2)中的另一名选手胜出，根据图表中的信息，应该制定怎样的评判规则？为什么？

Answer 1

答案：
解析：

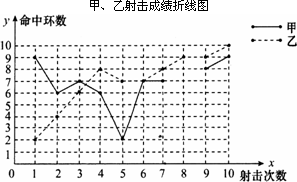
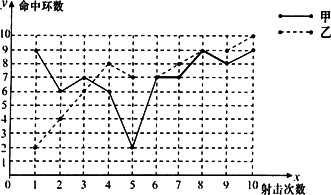
解：(1)根据折线统计图得： 　　乙的射击成绩为2，4，6，8，7，7，8，9，9，10， 　　则乙的平均数为(2＋4＋6＋8＋7＋7＋8＋9＋9＋10)÷10＝7(环)，中位数为7.5环，方差为×[(2－7)2＋(4－7)2＋(6－7)2＋(8－7)2＋(7－7)2＋(7－7)2＋(8－7)2＋(9－7)2＋(9－7)2＋(10－7)2]＝5.4； 　　甲的射击成绩为9，6，7，6，2，7，7，？，8，9，因为甲的平均数为7环， 　　所以甲的第八环成绩为70－(9＋6＋7＋6＋2＋7＋7＋8＋9)＝9(环)， 　　所以甲的10次射击成绩为9，6，7，6，2，7，7，9，8，9． 　　中位数为7环，方差为×[(9－7)2＋(6－7)2＋(7－7)2＋(6－7)2＋(2－7)2＋(7－7)2＋(7－7)2＋(9－7)2＋(8－7)2＋(9－7)2]＝4． 　　补全图表如下： 　　甲、乙射击成绩统计表 　　甲、乙射击成绩折线图 　　(2)甲胜出．理由如下：由于甲的方差小于乙的方差，所以甲的成绩比较稳定，故甲胜出． 　　(3)如果希望乙胜出，应该制定的评判规则为：平均成绩高的胜出；如果平均成绩相同，则随着比赛的进行，发挥越来越好者或命中满环(10环)次数多者胜出．因为甲、乙的平均成绩相同，乙只有第5次射击比第4次射击少命中1环，且命中1次10环，而甲第2次比第1次、第4次比第3次，第5次比第4次命中环数都低，且命中10环的次数为0次，即随着比赛的进行，乙的射击成绩越来越好．