题目内容
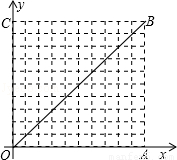
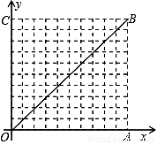
如图14,在平面直角坐标系中,点A的坐标为(m,m),点B的坐标为(n,![]() ),
),
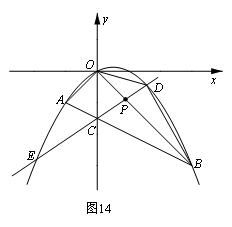 抛物线经过A、O、B三点,连结OA、OB、AB,线段AB交y轴于点C.已知实数m、
抛物线经过A、O、B三点,连结OA、OB、AB,线段AB交y轴于点C.已知实数m、
n(m<n)分别是方程![]() 的两根.
的两根.
(1)求抛物线的解析式;
(2)若点P为线段OB上的一个动点(不与点O、
B重合),直线PC与抛物线交于D、E两点
(点D在![]() 轴右侧),连结OD、BD.
轴右侧),连结OD、BD.
① 当△OPC为等腰三角形时,求点P的坐标;
② 求△BOD 面积的最大值,并写出此时点D
的坐标.
解(1)解方程![]() ,得
,得 ![]() ,
,![]() .
.
∵![]() ,∴
,∴![]() ,
,![]() ………………………………………………(1分)
………………………………………………(1分)
∴A(-1,-1),B(3,-3).
∵抛物线过原点,设抛物线的解析式为![]() .
.
∴![]() 解得
解得![]() ,
,![]() .
.
∴抛物线的解析式为![]() . ………………………………(4分)
. ………………………………(4分)
(2)①设直线AB的解析式为![]() .
.
 ∴
∴![]() 解得
解得![]() ,
,![]() .
.
∴直线AB的解析式为![]() .
.
∴C点坐标为(0,![]() ).………………(6分)
).………………(6分)
∵直线OB过点O(0,0),B(3,-3),
∴直线OB的解析式为![]() .
.
∵△OPC为等腰三角形,∴OC=OP或OP=PC或OC=PC.
设![]() ,
,![]() ,
,
(i)当OC=OP时, ![]() .
.
解得![]() ,
,![]() (舍去). ∴ P
(舍去). ∴ P![]() (
(![]() ,
, ![]() ).
).
(ii)当OP=PC时,点P在线段OC的中垂线上,∴ ![]() (
(![]() ,
,![]() .
.
(iii)当OC=PC时,由![]() ,
,
解得![]() ,
,![]() (舍去). ∴ P
(舍去). ∴ P![]() (
(![]() .
.
∴P点坐标为P![]() (
(![]() ,
,![]() )或
)或![]() (
(![]() ,
,![]() 或P
或P![]() (
(![]() .…(9分)
.…(9分)
②过点D作DG⊥x轴,垂足为G,交OB于Q,过B作BH⊥x轴,垂足为H.
设Q(![]() ,
,![]() ),D(
),D(![]() ,
,![]() ).
).
![]() =
=![]()
=![]() =
=![]() ,
,
∵0<![]() <3,
<3,
∴当![]() 时,S取得最大值为
时,S取得最大值为![]() ,此时D(
,此时D(![]() ,
,![]() .………………(13分)
.………………(13分)

练习册系列答案
相关题目
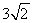
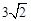 ,且这两个交点与抛物线的顶点是抛物线的内接格点三角形的三个顶点,则满足上述条件且对称轴平行于y轴的抛物线条数是
,且这两个交点与抛物线的顶点是抛物线的内接格点三角形的三个顶点,则满足上述条件且对称轴平行于y轴的抛物线条数是