题目内容
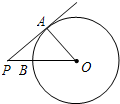如图，PA为⊙O的切线，A为切点，PO交⊙O于点B，PA=4，OA=3，则sin∠AOP的值为
- A.
- B.
- C.
- D.
C
分析：根据切线的性质，△OAP是直角三角形，根据勾股定理就可以求出OP=5，则可以求得sin∠AOP的值．
解答：∵PA为⊙O的切线，A为切点，
∴OA⊥AP，
∴∠PAO=90°，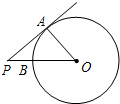
∴△PAO是直角三角形，
又∵PA=4，OA=3，
∴OP=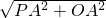
=5，
∴sin∠AOP=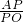
=．
故本题选C．
点评：本题运用了切线的性质定理，通过切线的性质定理得到△OAP是直角三角形，是解决本题的关键．
分析：根据切线的性质，△OAP是直角三角形，根据勾股定理就可以求出OP=5，则可以求得sin∠AOP的值．
解答：∵PA为⊙O的切线，A为切点，
∴OA⊥AP，
∴∠PAO=90°，
∴△PAO是直角三角形，
又∵PA=4，OA=3，
∴OP=
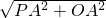=5，∴sin∠AOP=
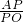=．故本题选C．
点评：本题运用了切线的性质定理，通过切线的性质定理得到△OAP是直角三角形，是解决本题的关键．
练习册系列答案
阅读快车系列答案
相关题目
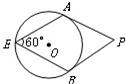7、如图，PA、PB分别切⊙O于点A、B，点E是⊙O上一点，且∠AEB=60°，则∠P的度数为（ ）
4、如图，PA、PB分别切⊙O于A、B两点，如果∠P=60°，PA=2，那么AB的长为（ ）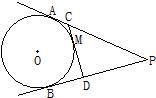
6、如图，PA、PB分别切⊙O于点A、B，M是劣弧AB上的一个动点（点A、B除外），过M作⊙O的切线分别交PA、PB于点C、D．设CM的长为x，△PCD的周长为y，在下列图象中，大致表示y与x之间的函数关系的是（ ）
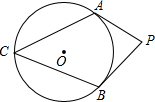（2012•莆田质检）如图，PA、PB分别切⊙O于A、B两点，点C在优弧
如图，PA，PB分别切⊙O于点A和点B，C是