题目内容
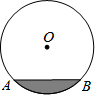 如图,直径为20cm,截面为圆的水槽⊙O中有一些水,此时水面宽AB=12cm,后来水面上升了一定距离,但仍没有超过圆心,此时水面宽AB=16cm,则水面上升了
如图,直径为20cm,截面为圆的水槽⊙O中有一些水,此时水面宽AB=12cm,后来水面上升了一定距离,但仍没有超过圆心,此时水面宽AB=16cm,则水面上升了2
2
cm.分析:先连接OA,OA1,根据直径为20cm,得出OA=OA1=10,再根据OE⊥AB,AB=12cm,利用勾股定理求出OE的长,同理得出OD的长,最后根据DE=OE-OD,即可得出答案.
解答:解: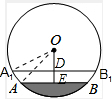 根据题意如图:
根据题意如图:
连接OA,OA1,
∵直径为20cm,
∴OA=OA1=10,
∵OE⊥AB,AB=12cm,
∴AE=6,
∴OE=
=
=8(cm).
∵A1B1=16cm,
∴A1D=8,
∴OD=
=
=6(cm),
∴DE=OE-OD=8-6=2(cm).
∴水面上升了2cm.
故答案为:2.
 根据题意如图:
根据题意如图:连接OA,OA1,
∵直径为20cm,
∴OA=OA1=10,
∵OE⊥AB,AB=12cm,
∴AE=6,
∴OE=
| OA2-OE2 |
| 102-62 |
∵A1B1=16cm,
∴A1D=8,
∴OD=
| OA12-A1D2 |
| 102-82 |
∴DE=OE-OD=8-6=2(cm).
∴水面上升了2cm.
故答案为:2.
点评:此题考查了垂经定理与勾股定理,用到的知识点是勾股定理、垂经定理,关键是根据题意作出辅助线,构造直角三角形.

练习册系列答案
相关题目
一只封闭的圆柱形水桶(桶的厚度忽略不计),底面直径为20cm,母线长为40cm,盛了半桶水,现将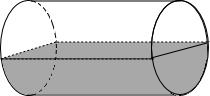 该水桶水平放置后如图所示,则水所形成的几何体的表面积为( )
该水桶水平放置后如图所示,则水所形成的几何体的表面积为( )
 该水桶水平放置后如图所示,则水所形成的几何体的表面积为( )
该水桶水平放置后如图所示,则水所形成的几何体的表面积为( )| A、800cm2 | B、(800+400π)cm2 | C、(800+500π)cm2 | D、(1600+1200π)cm2 |
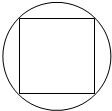 用一根铁丝做成一个正方形,使它恰好能嵌入一个直径为20cm的圆中(如图),求这根铁丝的长度.(结果精确到0.1cm)
用一根铁丝做成一个正方形,使它恰好能嵌入一个直径为20cm的圆中(如图),求这根铁丝的长度.(结果精确到0.1cm)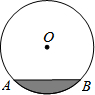 如图,直径为20cm,截面为圆的水槽⊙O中有一些水,此时水面宽AB=12cm,后来水面上升了一定距离,但仍没有超过圆心,此时水面宽AB=16cm,则水面上升了________cm.
如图,直径为20cm,截面为圆的水槽⊙O中有一些水,此时水面宽AB=12cm,后来水面上升了一定距离,但仍没有超过圆心,此时水面宽AB=16cm,则水面上升了________cm.