题目内容
(2009•厦门质检)已知关于x的一元二次方程 x2-2x+a(x+a)=0的两个实数根为x1,x2,若y=x1+x2+
x2-2x+a(x+a)=0的两个实数根为x1,x2,若y=x1+x2+
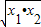 .
.(1)当a≥0时,求y的取值范围;
(2)当a≤-2时,比较y与-a2+6a-4的大小,并说明理由.
【答案】分析:(1)用根的判别式确定a的取值范围,根据根与系数的关系用a表示y,确定y的取值范围.
(2)根据a的取值范围确定y及代数式-a2+6a-4的取值范围,可比较其大小.
解答:解:(1)由 x2-2x+a(x+a)=0得,
x2-2x+a(x+a)=0得,
 x2+(a-2)x+a2=0
x2+(a-2)x+a2=0
△=(a-2)2-4× ×a2
×a2
=-4a+4
∵方程有两个实数根,
∴-4a+4≥0.
∴a≤1
∵a≥0
∴0≤a≤1
∴y=x1+x2+
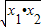
=-4a+8+a
=-3a+8
∵-3≤0,
∴y随a的增大而减小
当a=0时,y=8;a=1时,y=5
∴5≤y≤8.
(2)由(1)得a≤1,又a≤-2,
∴a≤-2
∴y=x1+x2+
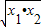
=-4a+8-a
=-5a+8
当a=-2时,y=18;
∵-3≤0
∴y随a的增大而减小.
∴当a≤-2时,y≥18
又∵-a2+6a-4=-(a-3)2+5≤5
而18>5
∴当a≤-2时,y>-a2+6a-4
点评:考查用根的判别式求取值范围,一元二次方程根与系数的关系以及一次函数的性质的综合运用.
(2)根据a的取值范围确定y及代数式-a2+6a-4的取值范围,可比较其大小.
解答:解:(1)由
 x2-2x+a(x+a)=0得,
x2-2x+a(x+a)=0得, x2+(a-2)x+a2=0
x2+(a-2)x+a2=0△=(a-2)2-4×
 ×a2
×a2=-4a+4
∵方程有两个实数根,
∴-4a+4≥0.
∴a≤1
∵a≥0
∴0≤a≤1
∴y=x1+x2+

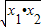
=-4a+8+a
=-3a+8
∵-3≤0,
∴y随a的增大而减小
当a=0时,y=8;a=1时,y=5
∴5≤y≤8.
(2)由(1)得a≤1,又a≤-2,
∴a≤-2
∴y=x1+x2+

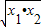
=-4a+8-a
=-5a+8
当a=-2时,y=18;
∵-3≤0
∴y随a的增大而减小.
∴当a≤-2时,y≥18
又∵-a2+6a-4=-(a-3)2+5≤5
而18>5
∴当a≤-2时,y>-a2+6a-4
点评:考查用根的判别式求取值范围,一元二次方程根与系数的关系以及一次函数的性质的综合运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
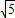 .将直线y=-3x+6绕点A旋转,记点B的对应点是B1,
.将直线y=-3x+6绕点A旋转,记点B的对应点是B1,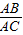 =
= ,求AC的长;
,求AC的长;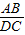 =
= ,求tanC的值.
,求tanC的值.