题目内容
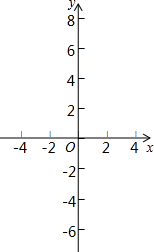 (2012•顺义区二模)如图,在平面直角坐标系xOy中,二次函数y=
(2012•顺义区二模)如图,在平面直角坐标系xOy中,二次函数y=| 1 |
| 2 |
(1)求二次函数的解析式;
(2)设D为线段OC上的一点,若∠DPC=∠BAC,求点D的坐标;
(3)在(2)的条件下,若点M在抛物线y=
| 1 |
| 2 |
分析:(1)将点A及点B的坐标代入二次函数解析式即可得出b和c的值,继而可得出函数解析式;
(2)先求出点C的坐标,根据二次函数解析式求出点P的坐标,然后可得出∠ACB=∠PCD=45°,结合∠DPC=∠BAC,可判断△ACB∽△PCD,利用相似三角形的性质求出CD,然后求出OD,即可得出点D的坐标;
(3)①当BD为平行四边形的一边时,根据平行四边形的性质可得BD=
=MN,结合点N在y轴上,可得出点M的横坐标为
或-
,代入函数解析式即可得出点M的坐标;
②当BD为对角线时,根据点N的横坐标为0,可得出点M的横坐标为
,代入可得出点M的坐标.
(2)先求出点C的坐标,根据二次函数解析式求出点P的坐标,然后可得出∠ACB=∠PCD=45°,结合∠DPC=∠BAC,可判断△ACB∽△PCD,利用相似三角形的性质求出CD,然后求出OD,即可得出点D的坐标;
(3)①当BD为平行四边形的一边时,根据平行四边形的性质可得BD=
| 8 |
| 3 |
| 8 |
| 3 |
| 8 |
| 3 |
②当BD为对角线时,根据点N的横坐标为0,可得出点M的横坐标为
| 2 |
| 3 |
解答:解:(1)将点A(-3,6),B(-1,0)代入y=
x2+bx+c中,
得
,
解得
,
∴二次函数的解析式为y=
x2-x-
.
(2)令y=0,得
x2-x-
=0,解得 x1=-1,x2=3,
则点C的坐标为(3,0),

∵y=
x2-x-
=
(x-1)2-2,
∴顶点P的坐标为(1,-2).
过点A作AE⊥x轴,过点P作PF⊥x轴,垂足分别为E,F,
易得∠ACB=∠PCD=45°,
AC=
=6
,PC=
=2
,
又∵∠DPC=∠BAC,
∴△ACB∽△PCD,
∴
=
,
∵BC=3-(-1)=4,
∴CD=
=
,
∴OD=OC-CD=3-
=
,
∴点D的坐标为(
, 0).
(3)①当BD为一边时,由于BD=
,此时可得点M的横坐标为
或-
,代入函数解析式y=
x2-x-
,
可得点M的坐标为(-
,
)或(
, -
).
②当BD为对角线时,根据对角线互相平分,可得平行四边形的中心的坐标为(
,0)
由∵点N的横坐标为0,
∴点M的横坐标为
,代入函数解析式可得此时点M的坐标为(
, -
).
综上可得点M的坐标为:(
,-
)或(-
,
)或(
,-
).
| 1 |
| 2 |
得
|
解得
|
∴二次函数的解析式为y=
| 1 |
| 2 |
| 3 |
| 2 |
(2)令y=0,得
| 1 |
| 2 |
| 3 |
| 2 |
则点C的坐标为(3,0),

∵y=
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
∴顶点P的坐标为(1,-2).
过点A作AE⊥x轴,过点P作PF⊥x轴,垂足分别为E,F,
易得∠ACB=∠PCD=45°,
AC=
| AE2+CE2 |
| 2 |
| PF2+CF2 |
| 2 |
又∵∠DPC=∠BAC,
∴△ACB∽△PCD,
∴
| BC |
| CD |
| AC |
| PC |
∵BC=3-(-1)=4,
∴CD=
| BC•PC |
| AC |
| 4 |
| 3 |
∴OD=OC-CD=3-
| 4 |
| 3 |
| 5 |
| 3 |
∴点D的坐标为(
| 5 |
| 3 |
(3)①当BD为一边时,由于BD=
| 8 |
| 3 |
| 8 |
| 3 |
| 8 |
| 3 |
| 1 |
| 2 |
| 3 |
| 2 |
可得点M的坐标为(-
| 8 |
| 3 |
| 85 |
| 18 |
| 8 |
| 3 |
| 11 |
| 18 |
②当BD为对角线时,根据对角线互相平分,可得平行四边形的中心的坐标为(
| 1 |
| 3 |
由∵点N的横坐标为0,
∴点M的横坐标为
| 2 |
| 3 |
| 2 |
| 3 |
| 35 |
| 18 |
综上可得点M的坐标为:(
| 8 |
| 3 |
| 11 |
| 18 |
| 8 |
| 3 |
| 85 |
| 18 |
| 2 |
| 3 |
| 35 |
| 18 |
点评:此题属于二次函数的综合题,涉及了待定系数法求函数解析式、相似三角形的判定与性质、平行四边形的性质,难度较大,难点在第二问,关键是判断出△ACB∽△PCD,求出OD的长度,第三问解答的关键之处在于分类讨论,得出点M的横坐标.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
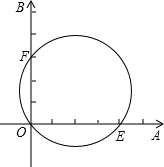 (2012•顺义区二模)如图,小华同学设计了一个圆直径的测量器,把标有刻度的尺子OA、OB在O点钉在一起,并使它们保持互相垂直.在测直径时,把O点靠在圆周上,读得刻度OE=4个单位,OF=3个单位,则圆的直径为( )
(2012•顺义区二模)如图,小华同学设计了一个圆直径的测量器,把标有刻度的尺子OA、OB在O点钉在一起,并使它们保持互相垂直.在测直径时,把O点靠在圆周上,读得刻度OE=4个单位,OF=3个单位,则圆的直径为( )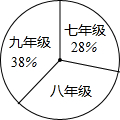 图,其中八年级学生人数为204人,请你根据图表中提供的信息,解答下列问题:
图,其中八年级学生人数为204人,请你根据图表中提供的信息,解答下列问题: