题目内容
 (2012•义乌市)如图,已知抛物线y1=-2x2+2,直线y2=2x+2,当x任取一值时,x对应的函数值分别为y1、y2.若y1≠y2,取y1、y2中的较小值记为M;若y1=y2,记M=y1=y2.例如:当x=1时,y1=0,y2=4,y1<y2,此时M=0.下列判断:
(2012•义乌市)如图,已知抛物线y1=-2x2+2,直线y2=2x+2,当x任取一值时,x对应的函数值分别为y1、y2.若y1≠y2,取y1、y2中的较小值记为M;若y1=y2,记M=y1=y2.例如:当x=1时,y1=0,y2=4,y1<y2,此时M=0.下列判断:①当x>0时,y1>y2; ②当x<0时,x值越大,M值越小;
③使得M大于2的x值不存在; ④使得M=1的x值是-
| 1 |
| 2 |
| ||
| 2 |
其中正确的是( )
分析:利用图象与坐标轴交点以及M值的取法,分别利用图象进行分析即可得出答案.
解答:解:∵当x>0时,利用函数图象可以得出y2>y1;∴①错误;
∵抛物线y1=-2x2+2,直线y2=2x+2,当x任取一值时,x对应的函数值分别为y1、y2.若y1≠y2,取y1、y2中的较小值记为M;
∴当x<0时,根据函数图象可以得出x值越大,M值越大;∴②错误;
∵抛物线y1=-2x2+2,直线y2=2x+2,与y轴交点坐标为:(0,2),当x=0时,M=2,抛物线y1=-2x2+2,最大值为2,故M大于2的x值不存在;
∴使得M大于2的x值不存在,∴③正确;
∵当-1<x<0时,
使得M=1时,可能是y1=-2x2+2=1,解得:x1=
,x2=-
,
当y2=2x+2=1,解得:x=-
,
由图象可得出:当x=
>0,此时对应y1=M,
∵抛物线y1=-2x2+2与x轴交点坐标为:(1,0),(-1,0),
∴当-1<x<0,此时对应y2=M,
故M=1时,x1=
,x2=-
,
使得M=1的x值是-
或
.∴④正确;
故正确的有:③④.
故选:D.
∵抛物线y1=-2x2+2,直线y2=2x+2,当x任取一值时,x对应的函数值分别为y1、y2.若y1≠y2,取y1、y2中的较小值记为M;
∴当x<0时,根据函数图象可以得出x值越大,M值越大;∴②错误;
∵抛物线y1=-2x2+2,直线y2=2x+2,与y轴交点坐标为:(0,2),当x=0时,M=2,抛物线y1=-2x2+2,最大值为2,故M大于2的x值不存在;
∴使得M大于2的x值不存在,∴③正确;
∵当-1<x<0时,
使得M=1时,可能是y1=-2x2+2=1,解得:x1=
| ||
| 2 |
| ||
| 2 |
当y2=2x+2=1,解得:x=-
| 1 |
| 2 |
由图象可得出:当x=
| ||
| 2 |
∵抛物线y1=-2x2+2与x轴交点坐标为:(1,0),(-1,0),
∴当-1<x<0,此时对应y2=M,
故M=1时,x1=
| ||
| 2 |
| 1 |
| 2 |
使得M=1的x值是-
| 1 |
| 2 |
| ||
| 2 |
故正确的有:③④.
故选:D.
点评:此题主要考查了二次函数与一次函数综合应用,利用数形结合得出函数增减性是解题关键.

练习册系列答案
相关题目
 (2012•义乌市)如图,矩形OABC的顶点A、C分别在x、y轴的正半轴上,点D为对角线OB的中点,点E(4,n)在边AB上,反比例函数
(2012•义乌市)如图,矩形OABC的顶点A、C分别在x、y轴的正半轴上,点D为对角线OB的中点,点E(4,n)在边AB上,反比例函数 (2012•义乌市模拟)如图,DE是△ABC的中位线,DE=2cm,则BC=
(2012•义乌市模拟)如图,DE是△ABC的中位线,DE=2cm,则BC=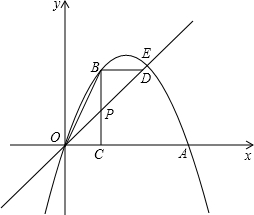 (2012•义乌市模拟)已知抛物线
(2012•义乌市模拟)已知抛物线