Question

【题目】在矩形ABCD中，AB＝6，AD＝9，点E为线段AD上一点，且DE＝2AE，点G是线段AB上的动点，EF⊥EG交BC所在直线于点F，连接GF．则GF的最小值是（　　）

A.3B.6C.6D.3

Answer 1

【答案】D

【解析】

过点F作FM⊥AD于M，证△AEG∽△MEF，设AG=x，利用相似的性质用含x的代数式表示EM的长度，在Rt△GBF中，利用勾股定理用含x的代数式表示出GF2，利用函数的性质求出其最小值，再求出GF的最小值即可．

解：如图，过点F作FM⊥AD于M，

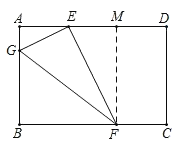
∵四边形ABCD为矩形，

∴∠A＝∠EMF＝90°，MF＝AB＝6，

∵EF⊥GE，

∴∠AGE+∠AEG＝90°，∠AEG+∠MEF＝90°，

∴∠AGE＝∠MEF，

∴△AEG∽△MFE，

∴，

设AG＝x，

∵AD＝9，DE＝2AE，

∴AE＝3，

∴，

∴ME＝2x，

∴BF＝AM＝3+2x，

在Rt△GBF中，

GF2＝GB2+BF2

＝（6﹣x）2+（3+2x）2

＝5x2+45，

∵点G在线段AB上，

∴0≤x≤6，

由二次函数的性质可知，当x＝0时，GF2有最小值45，

∴GF的最小值为3，

故选D．