题目内容
一个正整数若能表示成两个正整数的平方差,则称这个正整数为“杨敏数”.例如,16=52-32就是一个“杨敏数”.则把所有的“杨敏数”从小到大排列后,第47个“杨敏数”是
- A.97
- B.95
- C.64
- D.65
D
分析:如果一个数是杨敏数,就能表示为两个正整数的平方差,设这两个数分别m、n,设m>n,即杨敏数=m2-n2=(m+n)(m-n),因为m,n是正整数,因而m+n和m-n就是两个自然数.要判断一个数是否是杨敏数,可以把这个数分解因数,分解成两个整数的积,看这两个数能否写成两个正整数的和与差.
解答:1不能表示为两个正整数的平方差,所以1不是“杨敏数”.对于大于1的奇正整数2k+1,有2k+1=(k+1)2-k2(k=1,2,…).
所以大于1的奇正整数都是“杨敏数”.
对于被4整除的偶数4k,有4k=(k+1)2-(k-1)2(k=2,3,…).
即大于4的被4整除的数都是“杨敏数”,而4不能表示为两个正整数平方差,所以4不是“杨敏数”.
对于被4除余2的数4k+2(k=0,1,2,3,…),设4k+2=x2-y2=(x+y)(x-y),其中x,y为正整数,
当x,y奇偶性相同时,(x+y)(x-y)被4整除,而4k+2不被4整除;
当x,y奇偶性相异时,(x+y)(x-y)为奇数,而4k+2为偶数,总得矛盾.
所以不存在自然数x,y使得x2-y2=4k+2.即形如4k+2的数均不为“杨敏数”.
因此,在正整数数列中前四个正整数只有3为“杨敏数”,此后,每连续四个数中有三个“杨敏数”.
∵47=(1+3×15)+1,4×(15+1)=64,64是第46个“杨敏数”,
65是第47个“杨敏数”.
故选:D.
点评:此题主要考查了平方差公式,有一定的难度,主要是对题中新定义的理解与把握.
分析:如果一个数是杨敏数,就能表示为两个正整数的平方差,设这两个数分别m、n,设m>n,即杨敏数=m2-n2=(m+n)(m-n),因为m,n是正整数,因而m+n和m-n就是两个自然数.要判断一个数是否是杨敏数,可以把这个数分解因数,分解成两个整数的积,看这两个数能否写成两个正整数的和与差.
解答:1不能表示为两个正整数的平方差,所以1不是“杨敏数”.对于大于1的奇正整数2k+1,有2k+1=(k+1)2-k2(k=1,2,…).
所以大于1的奇正整数都是“杨敏数”.
对于被4整除的偶数4k,有4k=(k+1)2-(k-1)2(k=2,3,…).
即大于4的被4整除的数都是“杨敏数”,而4不能表示为两个正整数平方差,所以4不是“杨敏数”.
对于被4除余2的数4k+2(k=0,1,2,3,…),设4k+2=x2-y2=(x+y)(x-y),其中x,y为正整数,
当x,y奇偶性相同时,(x+y)(x-y)被4整除,而4k+2不被4整除;
当x,y奇偶性相异时,(x+y)(x-y)为奇数,而4k+2为偶数,总得矛盾.
所以不存在自然数x,y使得x2-y2=4k+2.即形如4k+2的数均不为“杨敏数”.
因此,在正整数数列中前四个正整数只有3为“杨敏数”,此后,每连续四个数中有三个“杨敏数”.
∵47=(1+3×15)+1,4×(15+1)=64,64是第46个“杨敏数”,
65是第47个“杨敏数”.
故选:D.
点评:此题主要考查了平方差公式,有一定的难度,主要是对题中新定义的理解与把握.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
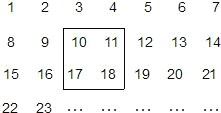
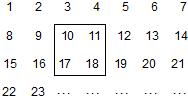
 把2013个正整数1,2,3,4,…,2013按如图方式排列成一个表.
把2013个正整数1,2,3,4,…,2013按如图方式排列成一个表.