题目内容
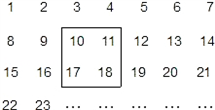
把2008个正整数1,2,3,4,…,2008按如图方式排列成一个表.(1)如图,用一正方形框,在表中任意框住4个数,记左上角的一个数为x,则这4个数的和是
(2)当(1)中被框住的4个数之和等于216时,x的值为多少?
(3)在(1)中能否框住这样的4个数,它们的和等于296?若能,则求出x的值;若不能,则说明理由.
(4)从左到右,第1至第7列各列的所有数之和分别记为a1,a2,a3,a4,a5,a6,a7,则这7个数中,最大数与最小数之差等于
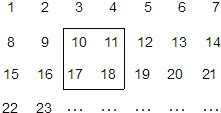
分析:(1)由题中关系,可知左上角的一个数为x,则另3个数分别为x+1;x+7;x+8.求四个代数式的和即可.
(2)根据题(1)中的代数式,列出等式求x的解即可.
(3)按照(2)的思路,求x的解即可.注意解需要满足图中的规律.
(4)根据规律找出最大数和最小数,求差即可.
(2)根据题(1)中的代数式,列出等式求x的解即可.
(3)按照(2)的思路,求x的解即可.注意解需要满足图中的规律.
(4)根据规律找出最大数和最小数,求差即可.
解答:解:(1)已知左上角的一个数为x,则另3个数分别为x+1;x+7;x+8,则四数之和为4x+16.
(2)当4个数之和等于216时,则4x+16=216,解得x=50.
(3)不能;当4个数之和等于296时,
设4x+16=296,解得x=70;
但左上角的x不能为7的倍数,故四数之和不能为296.
(4)填1722.
因为数2008在第287行第6列,所以可知a6最大,a7最小,a6-a7=2008-(
)×1=1722.
(2)当4个数之和等于216时,则4x+16=216,解得x=50.
(3)不能;当4个数之和等于296时,
设4x+16=296,解得x=70;
但左上角的x不能为7的倍数,故四数之和不能为296.
(4)填1722.
因为数2008在第287行第6列,所以可知a6最大,a7最小,a6-a7=2008-(
| 2002 |
| 7 |
点评:本题考查了列代数式及其应用,还考查了同学们的寻找规律总结规律的能力,是一道考查综合能力的好题.

练习册系列答案
相关题目
 把2008个正整数1,2,3,4,…,2008按如图方式排列成一个表.
把2008个正整数1,2,3,4,…,2008按如图方式排列成一个表.