题目内容
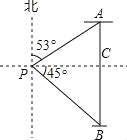
【题目】如图,一艘货轮位于灯塔P北偏东53°方向,距离灯塔100海里的A处,另一艘客轮位于货轮正南方向,且在灯塔P南偏东45°方向的B处,求此时两艘轮船之间的距离AB.(结果精确到1海里)
【参考数据:sin53°=0.799,cos53°=0.602,tan53°=1.327】

【答案】两艘轮船之间的距离AB约为140海里.
【解析】
试题分析:通过解直角△ACP得到AC、PC的长度;然后结合等腰直角三角形的性质来求BC的长度,则易求AB=AC+BC.
试题解析:由题意,得∠A=53°,BC=PC.
在直角△APC中,AC=100cos53°=100×0.602=60.2,
BC=PC=100sin53°=100×0.799=79.9,
所以AB=AC+BC=60.2+79.9=140.1≈140(海里).
答:两艘轮船之间的距离AB约为140海里.

练习册系列答案
 新编小学单元自测题系列答案
新编小学单元自测题系列答案 字词句段篇系列答案
字词句段篇系列答案
相关题目