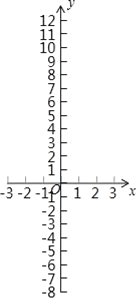题目内容
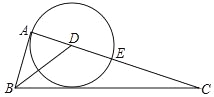
【题目】如图,△ABC中,∠A=90°,AB=AC=4,D是BC边上一点,将点D绕点A逆时针旋转60°得到点E,连接CE.
![]()

(1)当点E在BC边上时,画出图形并求出∠BAD的度数;
(2)当△CDE为等腰三角形时,求∠BAD的度数;
(3)在点D的运动过程中,求CE的最小值.
(参考数值:sin75°=![]() , cos75°=
, cos75°=![]() ,tan75°=
,tan75°=![]() )
)
【答案】(1)∠BAD=15°;(2)∠BAC=45°或∠BAD =60°;(3)CE=![]() .
.
【解析】
(1)如图1中,当点E在BC上时.只要证明△BAD≌△CAE,即可推出∠BAD=∠CAE=![]() (90°-60°)=15°;
(90°-60°)=15°;
(2)分两种情形求解①如图2中,当BD=DC时,易知AD=CD=DE,此时△DEC是等腰三角形.②如图3中,当CD=CE时,△DEC是等腰三角形;
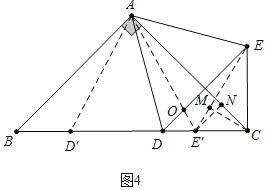
(3)如图4中,当E在BC上时,E记为E′,D记为D′,连接EE′.作CM⊥EE′于M,E′N⊥AC于N,DE交AE′于O.首先确定点E的运动轨迹是直线EE′(过点E与BC成60°角的直线上),可得EC的最小值即为线段CM的长(垂线段最短).
解:(1)如图1中,当点E在BC上时.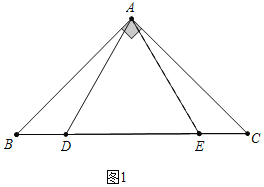
∵AD=AE,∠DAE=60°,
∴△ADE是等边三角形,
∴∠ADE=∠AED=60°,
∴∠ADB=∠AEC=120°,
∵AB=AC,∠BAC=90°,
∴∠B=∠C=45°,
在△ABD和△ACE中,
∠B=∠C,∠ADB=∠AEC,AB=AC,
∴△BAD≌△CAE,
∴∠BAD=∠CAE=![]() (90°-60°)=15°.
(90°-60°)=15°.
(2)①如图2中,当BD=DC时,易知AD=CD=DE,此时△DEC是等腰三角形,∠BAD=![]() ∠BAC=45°.
∠BAC=45°.
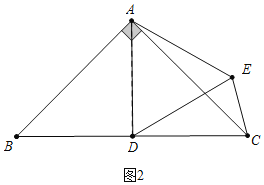
②如图3中,当CD=CE时,△DEC是等腰三角形.
∵AD=AE,
∴AC垂直平分线段DE,
∴∠ACD=∠ACE=45°,
∴∠DCE=90°,
∴∠EDC=∠CED=45°,
∵∠B=45°,
∴∠EDC=∠B,
∴DE∥AB,
∴∠BAD=∠ADE=60°.
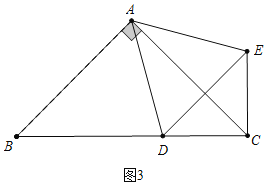
(3)如图4中,当E在BC上时,E记为E′,D记为D′,连接EE′.作CM⊥EE′于M,E′N⊥AC于N,DE交AE′于O.
∵∠AOE=∠DOE′,∠AE′D=∠AEO,
∴△AOE∽△DOE′,
∴AO:OD=EO:OE',
∴AO:EO=OD:OE',
∵∠AOD=∠EOE′,
∴△AOD∽△EOE′,
∴∠EE′O=∠ADO=60°,
∴点E的运动轨迹是直线EE′(过点E与BC成60°角的直线上),
∴EC的最小值即为线段CM的长(垂线段最短),
设E′N=CN=a,则AN=4-a,
在Rt△ANE′中,tan75°=AN:NE',
∴2+![]() =
=![]() ,
,
∴a=2-![]() ,
,
∴CE′=![]() CN=2
CN=2![]() -
-![]() .
.
在Rt△CE′M中,CM=CE′cos30°=![]() ,
,
∴CE的最小值为![]() .
.

 阅读快车系列答案
阅读快车系列答案【题目】佳佳向探究一元三次方程x3+2x2﹣x﹣2=0的解的情况,根据以往的学习经验,他想到了方程与函数的关系,一次函数y=kx+b(k≠0)的图象与x轴交点的横坐标即为一元一次方程kx+b(k≠0)的解,二次函数y=ax2+bx+c(a≠0)的图象与x轴交点的横坐标即为一元二次方程ax2+bx+c=0(a≠0)的解,如:二次函数y=x2﹣2x﹣3的图象与x轴的交点为(﹣1,0)和(3,0),交点的横坐标﹣1和3即为x2﹣2x﹣3=0的解.
根据以上方程与函数的关系,如果我们直到函数y=x3+2x2﹣x﹣2的图象与x轴交点的横坐标,即可知方程x3+2x2﹣x﹣2=0的解.
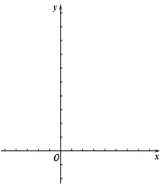
佳佳为了解函数y=x3+2x2﹣x﹣2的图象,通过描点法画出函数的图象.
x | … | ﹣3 | ﹣ | ﹣2 | ﹣ | ﹣1 | ﹣ | 0 |
| 1 |
| 2 | … |
y | … | ﹣8 | ﹣ | 0 |
| m | ﹣ | ﹣2 | ﹣ | 0 |
| 12 | … |
(1)直接写出m的值,并画出函数图象;
(2)根据表格和图象可知,方程的解有 个,分别为 ;
(3)借助函数的图象,直接写出不等式x3+2x2>x+2的解集.