题目内容
我们通过计算发现:抛物线y=x2+2x-1的顶点(-1,-2)在抛物线y=-x2+2x+1上,同时抛物线y=-x2+2x+1的顶点(1,2)也在抛物线y=x2+2x-1上,这时我们称这两条抛物线是相关的.
(1)问:抛物线y=x2-2x-1与抛物线y=-x2-2x+1是否相关,并说明理由.
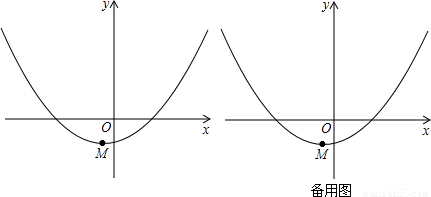
(2)如图,已知抛物线C:y= (x+1)2-2,顶点为M.
(x+1)2-2,顶点为M.
①若有一动点P的坐标为(m,2),现将抛物线C绕点P(m,2)旋转180°得到新的抛物线C′,且抛物线C与新的抛物线C′相关,求抛物线C′的解析式.
②若抛物线C′与C相关,顶点为N,现以MN为斜边作等腰直角△MNQ,问y轴上是否存在满足要求的点Q?若存在,求出Q点的坐标;若不存在,请说明理由.

解:(1)抛物线y=x2-2x-1的顶点坐标为:(1,-2);
抛物线y=-x2-2x+1的顶点坐标为:(-1,2);
①当x=1时,y=-x2-2x+1=-1-2+1=-2,∴点(1,-2)在抛物线y=-x2-2x+1上;
②当x=-1时,y=x2-2x-1=1+2-1=2,∴点(-1,2)在抛物线y=x2-2x-1上;
因此,抛物线y=x2-2x-1与抛物线y=-x2-2x+1相关.
(2)①抛物线C:y= (x+1)2-2的顶点M(-1,-2);
(x+1)2-2的顶点M(-1,-2);
由于抛物线C′是抛物线C绕点P(m,2)旋转180゜所得,所以抛物线C、C′的顶点关于点P对称,
∴抛物线C′的顶点坐标M′(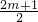 ,6),抛物线C′:y=-
,6),抛物线C′:y=- (x-
(x-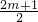 )2+6;
)2+6;
已知抛物线C和抛物线C′相关,那么点M′必在抛物线C的函数图象上,即:
6= (
(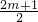 +1)2-2,解得:m1=
+1)2-2,解得:m1= 、m2=-
、m2=- ;
;
∴抛物线C′的解析式为:y=- (x-7)2+6或y=-
(x-7)2+6或y=- (x+9)2+6.
(x+9)2+6.
②由①得:点N的坐标为(7,6)或(-9,6);
已知:M(-1,-2),设点Q的坐标为(0,m),则:
当N点取(7,6)时,MN2=(7+1)2+(6+2)2=128、NQ2=(7-0)2+(6-m)2=m2-12m+85、MQ2=(-1-0)2+(-2-m)2=m2+4m+5
令,MQ2=NQ2,则 m2-12m+85=m2+4m+5,m=5
此时,MQ2+NQ2=50+50=100≠MN2
∴当N(7,6)时,不存在符合条件的Q点,使得△MNQ是等腰直角三角形;
同理可得:当N取(-9,6)时,也不存在符合条件的Q点;
综上,不存在符合条件的点Q,使得△MNQ是等腰直角三角形.
分析:(1)首先找出前后两个抛物线的顶点,然后将它们的顶点分别代入对方的抛物线解析式中进行验证,若各自的顶点分别在对方的抛物线图象上,即可确定两者相关,反之则不能.
(2)①抛物线C′是由抛物线C绕点P(m,2)旋转180゜所得,那么两条抛物线的顶点关于点P对称,据此求出抛物线C′的顶点坐标,若抛物线C、C′相关,那么抛物线C′的顶点必在抛物线C的函数图象上,因此只需将C′的顶点代入抛物线C中求解即可;
②在①中已求出抛物线C′的顶点,先设出点Q的坐标,然后由坐标系两点间的距离公式求出MQ2、NQ2、MN2,若△MNQ是以MN为斜边的等腰直角三角形,那么必须满足:MQ2=MN2,且MQ2+NQ2=MN2,若两式成立,那么存在符合条件的Q点,反之,则不存在.
点评:解答该题首先要充分理解题干资料所表达的含义,围绕二次函数的性质、图形的旋转、等腰直角三角型的判定和性质等重点知识对题目展开分析;(2)①的难度较大,找出两个抛物线顶点间的关系是突破题目的关键所在.此外,还要注意类似题目间的联系,如:将(2)②的“抛物线C′”改为“抛物线C″”时,解题的过程就会有很大不同,此时,可分别过M、N作y轴的垂线,通过构建全等三角形来得出点N的坐标.
抛物线y=-x2-2x+1的顶点坐标为:(-1,2);
①当x=1时,y=-x2-2x+1=-1-2+1=-2,∴点(1,-2)在抛物线y=-x2-2x+1上;
②当x=-1时,y=x2-2x-1=1+2-1=2,∴点(-1,2)在抛物线y=x2-2x-1上;
因此,抛物线y=x2-2x-1与抛物线y=-x2-2x+1相关.
(2)①抛物线C:y=
 (x+1)2-2的顶点M(-1,-2);
(x+1)2-2的顶点M(-1,-2);由于抛物线C′是抛物线C绕点P(m,2)旋转180゜所得,所以抛物线C、C′的顶点关于点P对称,
∴抛物线C′的顶点坐标M′(
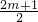 ,6),抛物线C′:y=-
,6),抛物线C′:y=- (x-
(x-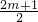 )2+6;
)2+6;已知抛物线C和抛物线C′相关,那么点M′必在抛物线C的函数图象上,即:
6=
 (
(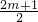 +1)2-2,解得:m1=
+1)2-2,解得:m1= 、m2=-
、m2=- ;
;∴抛物线C′的解析式为:y=-
 (x-7)2+6或y=-
(x-7)2+6或y=- (x+9)2+6.
(x+9)2+6.②由①得:点N的坐标为(7,6)或(-9,6);
已知:M(-1,-2),设点Q的坐标为(0,m),则:
当N点取(7,6)时,MN2=(7+1)2+(6+2)2=128、NQ2=(7-0)2+(6-m)2=m2-12m+85、MQ2=(-1-0)2+(-2-m)2=m2+4m+5
令,MQ2=NQ2,则 m2-12m+85=m2+4m+5,m=5
此时,MQ2+NQ2=50+50=100≠MN2
∴当N(7,6)时,不存在符合条件的Q点,使得△MNQ是等腰直角三角形;
同理可得:当N取(-9,6)时,也不存在符合条件的Q点;
综上,不存在符合条件的点Q,使得△MNQ是等腰直角三角形.
分析:(1)首先找出前后两个抛物线的顶点,然后将它们的顶点分别代入对方的抛物线解析式中进行验证,若各自的顶点分别在对方的抛物线图象上,即可确定两者相关,反之则不能.
(2)①抛物线C′是由抛物线C绕点P(m,2)旋转180゜所得,那么两条抛物线的顶点关于点P对称,据此求出抛物线C′的顶点坐标,若抛物线C、C′相关,那么抛物线C′的顶点必在抛物线C的函数图象上,因此只需将C′的顶点代入抛物线C中求解即可;
②在①中已求出抛物线C′的顶点,先设出点Q的坐标,然后由坐标系两点间的距离公式求出MQ2、NQ2、MN2,若△MNQ是以MN为斜边的等腰直角三角形,那么必须满足:MQ2=MN2,且MQ2+NQ2=MN2,若两式成立,那么存在符合条件的Q点,反之,则不存在.
点评:解答该题首先要充分理解题干资料所表达的含义,围绕二次函数的性质、图形的旋转、等腰直角三角型的判定和性质等重点知识对题目展开分析;(2)①的难度较大,找出两个抛物线顶点间的关系是突破题目的关键所在.此外,还要注意类似题目间的联系,如:将(2)②的“抛物线C′”改为“抛物线C″”时,解题的过程就会有很大不同,此时,可分别过M、N作y轴的垂线,通过构建全等三角形来得出点N的坐标.

练习册系列答案
 金博士一点全通系列答案
金博士一点全通系列答案
相关题目

 阅读并填空:
阅读并填空: (x+1)2-2,顶点为M.
(x+1)2-2,顶点为M.