题目内容
11、PA，PB是⊙O的切线，A，B为切点，若∠AOB=136°，则∠P=
44
度．分析：根据切线的性质知道∠OAP=∠OBP=90°，然后在四边形APBO中利用内角和定理就可以求出∠P的度数．
解答：解：∵PA，PB是⊙O的切线，
∴∠OAP=∠OBP=90°，
在四边形APBO中∠P=360°-∠OAP-∠OBP-∠AOB
=360°-180°-136°
=44°．
故填空答案：44°．
∴∠OAP=∠OBP=90°，
在四边形APBO中∠P=360°-∠OAP-∠OBP-∠AOB
=360°-180°-136°
=44°．
故填空答案：44°．
点评：本题主要考查了切线的性质，切线垂直于过切点的半径等知识，比较简单．
练习册系列答案
相关题目
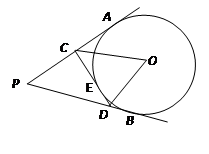
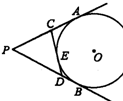
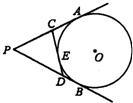7、如图，PA、PB是⊙O的两条切线，A、B是切点，CD切劣弧AB于点E，已知切线PA的长为6cm，则△PCD的周长为
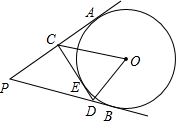如图，PA、PB是⊙O的切线，CD切⊙O于点E，△PCD的周长为12，∠APB=60°．求：
如图，PA、PB是⊙O的切线，点C在
