题目内容
已知关于 x的方程x2-（2k-3）+k2+1=0．
（1）当k为何值时，此方程有实数根；
（2）选择一个你喜欢的k的值，并求解此方程．
解：（1）要使方程有实数根，必须△≥0，
即（2k-3）2-4（k2+1）≥0，
解得k≤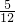
，
∴当k≤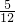时，方程有实数根．
（2）当k=0时，方程变为x2+3x+1=0
解得：x=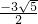
．
分析：（1）根据△≥0，确定k的取值范围；
（2）从上题中求得的范围中找到一个喜欢的值代入后得到方程，求解即可．
点评：本题考查的是一元二次方程根的判别式，熟知一元二次方程根的情况与判别式△的关系是解答此题的关键．
即（2k-3）2-4（k2+1）≥0，
解得k≤
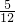，∴当k≤
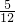时，方程有实数根．（2）当k=0时，方程变为x2+3x+1=0
解得：x=
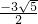．分析：（1）根据△≥0，确定k的取值范围；
（2）从上题中求得的范围中找到一个喜欢的值代入后得到方程，求解即可．
点评：本题考查的是一元二次方程根的判别式，熟知一元二次方程根的情况与判别式△的关系是解答此题的关键．
练习册系列答案
相关题目