Question

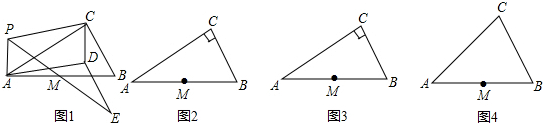
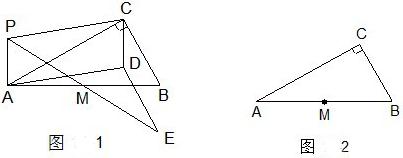
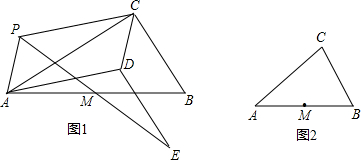
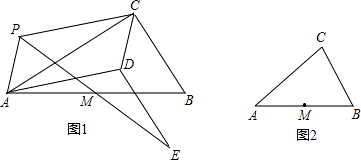
如图1，P为Rt△ABC所在平面内任一点（不在直线AC上），∠ACB=90°，M为AB的中点．
操作：以PA、PC为邻边作平行四边形PADC，连接PM并延长到点E，使ME=PM，连接DE．
（1）请你猜想与线段DE有关的三个结论，并证明你的猜想；
（2）若将“Rt△ABC”改为“任意△ABC”，其他条件不变，利用图2操作，并写出与线段DE有关的结论（直接写答案）．

Answer 1

（1）DE∥BC，DE=BC，DE⊥AC，
证明：连接BE，
∵M为AB中点，
∴AM=MB，
在△PMA和△EMB中
∵，
∴△PMA≌△EMB（SAS），
∴PA=BE，∠MPA=∠MEB，
∴PA∥BE．
∵四边形PADC是平行四边形，
∴PA∥DC，PA=DC，
∴BE∥DC，BE=DC，
∴四边形DEBC是平行四边形，
∴DE∥BC，DE=BC．
∵∠ACB=90°，
∴BC⊥AC，
∴DE⊥AC．

（2）解：DE∥BC，DE=BC．
分析：（1）连接BE，证△PMA≌△EMB，推出PA=BE，∠MPA=∠MEB，推出PA∥BE．根据平行四边形的性质得出PA∥DC，PA=DC，推出BE∥DC，BE=DC，得出平行四边形CDEB即可；
（2）连接BE，证△PMA≌△EMB，推出PA=BE，∠MPA=∠MEB，推出PA∥BE．根据平行四边形的性质得出PA∥DC，PA=DC，推出BE∥DC，BE=DC，得出平行四边形CDEB即可．
点评：本题考查了平行四边形性质和判定，全等三角形的性质和判定，平行线的性质和判定的综合运用．