题目内容
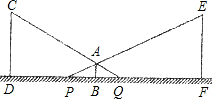 小明利用灯光下自己的影子长度来测量路灯的高度.如图,CD和EF是两等高的路灯,相距27m,身高1.5m的小明(AB)站在两路灯之间(D、B、F共线),被两路灯同时照射留在地面的影长BQ=4m,BP=5m.
小明利用灯光下自己的影子长度来测量路灯的高度.如图,CD和EF是两等高的路灯,相距27m,身高1.5m的小明(AB)站在两路灯之间(D、B、F共线),被两路灯同时照射留在地面的影长BQ=4m,BP=5m.(1)小明距离路灯多远?
(2)求路灯高度.
分析:(1)易得△QAB∽△QCD,那么可得
=
,同理可得
=
,根据CD=EF,可得一个比例式,把相关数值代入可得所求数值;
(2)根据(1)得到的比例式及数值,计算可得路灯高度.
| AB |
| CD |
| BQ |
| QD |
| AB |
| EF |
| BP |
| PF |
(2)根据(1)得到的比例式及数值,计算可得路灯高度.
解答:解:(1)设DB=xm,
∵AB∥CD,
∴∠QBA=∠QDC,∠QAB=∠QCD,
∴△QAB∽△QCD(2分)
∴
=
(3分)
同理可得
=
∵CD=EF
∴
=
(5分)
∴
=
∴x=12(7分)
即小明距离路灯12m.(8分)
(2)由
=
得
=
∴CD=6
即路灯高6m.(10分)
∵AB∥CD,
∴∠QBA=∠QDC,∠QAB=∠QCD,
∴△QAB∽△QCD(2分)
∴
| AB |
| CD |
| BQ |
| QD |
同理可得
| AB |
| EF |
| BP |
| PF |
∵CD=EF
∴
| BQ |
| QD |
| BP |
| PF |
∴
| 4 |
| x+4 |
| 5 |
| 5+(27-x) |
∴x=12(7分)
即小明距离路灯12m.(8分)
(2)由
| AB |
| CD |
| BQ |
| QD |
| 1.5 |
| CD |
| 4 |
| 4+12 |
∴CD=6
即路灯高6m.(10分)
点评:考查相似三角形的应用;利用线段相等得到相关比例式是解决本题的突破点.

练习册系列答案
相关题目
 剩下路程的
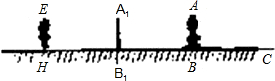
剩下路程的 学习投影后,小明、小颖利用灯光下自己的影子长度来测量一路灯的高度,并探究影子长度的变化规律.如图,在同一时间,身高为1.6m的小明(AB)的影子BC长是3m,而小颖(EH)刚好在路灯灯泡的正下方H点,并测得HB=6m.
学习投影后,小明、小颖利用灯光下自己的影子长度来测量一路灯的高度,并探究影子长度的变化规律.如图,在同一时间,身高为1.6m的小明(AB)的影子BC长是3m,而小颖(EH)刚好在路灯灯泡的正下方H点,并测得HB=6m. 小明利用灯光下自己的影子长度来测量路灯的高度.如图,CD和EF是两等高的路灯,相距27m,身高1.5rn的小明(AB)站在两路灯之间(D、B、F共线),被两路灯同时照射留在地面的影长BQ=4m,BP=5m.
小明利用灯光下自己的影子长度来测量路灯的高度.如图,CD和EF是两等高的路灯,相距27m,身高1.5rn的小明(AB)站在两路灯之间(D、B、F共线),被两路灯同时照射留在地面的影长BQ=4m,BP=5m.