题目内容
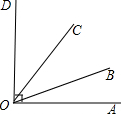
 如图,已知∠AOB与∠AOC互补,OD是∠AOB的平分线,∠COD=15°,求∠AOC的度数.
如图,已知∠AOB与∠AOC互补,OD是∠AOB的平分线,∠COD=15°,求∠AOC的度数.分析:设∠AOC=x,根据互补的定义得到∠AOB=180°-x°,再根据角平分线的定义得到∠AOD=
(180°-x),利用∠AOD-∠AOC=∠COD,则
(180°-x)-x=15°,然后解方程即可.
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:设∠AOC=x,
∵∠AOB与∠AOC互补,
∴∠AOB=180°-x°,
∵OD平分∠AOB,
∴∠AOD=
(180°-x),
∵∠AOD-∠AOC=∠COD,
∴
(180°-x)-x=15°,
解得 x=50,
∴∠AOC=50°.
∵∠AOB与∠AOC互补,
∴∠AOB=180°-x°,
∵OD平分∠AOB,
∴∠AOD=
| 1 |
| 2 |
∵∠AOD-∠AOC=∠COD,
∴
| 1 |
| 2 |
解得 x=50,
∴∠AOC=50°.
点评:本题考查了余角和补角:若两个角的和为90°,那么这两个角互余;若两个角的和为180°,那么这两个角互补.也考查了角平分线的定义.

练习册系列答案
相关题目
 如图:已知∠AOB与∠BOD互为余角,OC是∠BOD的角平分线,∠AOB=29.66°,∠COD的度数是( )
如图:已知∠AOB与∠BOD互为余角,OC是∠BOD的角平分线,∠AOB=29.66°,∠COD的度数是( )| A、30°17' | B、30.67° | C、30°10′12″ | D、30°10' |
 23、如图,已知△AOB与△DOC成中心对称,△AOB的面积是12,AB=3,则△DOC中CD边上的高是
23、如图,已知△AOB与△DOC成中心对称,△AOB的面积是12,AB=3,则△DOC中CD边上的高是 如图,已知∠AOB与∠COD都是∠BOC的余角,OE、OF分别是∠AOB、∠COD的平分线,∠BOC=50°,求∠AOD与∠EOF的度数.
如图,已知∠AOB与∠COD都是∠BOC的余角,OE、OF分别是∠AOB、∠COD的平分线,∠BOC=50°,求∠AOD与∠EOF的度数. 尺规作图.
尺规作图.