题目内容
【题目】如图,在Rt△ABC中,AC=4cm,BC=3cm,点P由B出发沿BA的方向向点A匀速运动,速度为1cm/s,同时点Q由A出发沿AC的方向向点C匀速运动,速度为2cm/s,连接PQ,设运动的时间为t(s),其中0<t<2,解答下列问题:

(1)当t为何值时,以P、Q、A为顶点的三角形与△ABC相似?
(2)是否存在某一时刻t,线段PQ将△ABC的面积分成1:2两部分?若存在,求出此时的t,若不存在,请说明理由;
(3)点P、Q在运动的过程中,△CPQ能否成为等腰三角形?若能,请求出此时t的值,若不存在,请说明理由.
【答案】(1)t=![]() 或
或![]() ;(2)存在,t=
;(2)存在,t=![]() ;(3)能,t=
;(3)能,t=![]() 或t=
或t=![]() .
.
【解析】
试题分析:(1)分两种情况讨论:①当∠PQA=∠C=90时,△PQA∽△BCA,由题意得:AB=5,PB=t,PA=5-t,AQ=2t,利用相似三角形对应边成比例,即![]() ,求出t值;②当∠QPA=∠C=90时,△PQA∽△CBA,由题意得:PA=5-t,AQ=2t,利用相似三角形对应边成比例,即
,求出t值;②当∠QPA=∠C=90时,△PQA∽△CBA,由题意得:PA=5-t,AQ=2t,利用相似三角形对应边成比例,即![]() ,求出t值;(2)先把三角形ABC的面积求出来,过点P作PH⊥CA,垂足为点H,利用三角形相似把高PH用含有t的式子表示出来,再把三角形APQ的面积用含有t的式子表示出来,若线段PQ将△ABC的面积能分成1:2两部分,则三角形APQ的面积等于△ABC面积的三分之一,或者三分之二,建立方程求解;(3)当△CPQ为等腰三角形时,分三种情况讨论:①当PC=PQ时,过点P作PH⊥CA,垂足为点H,利用△PHA∽△BCA,建立对应边成比例求出t值;②当CP=CQ时,过点P作PM⊥CB,垂足为点M,由△BMP∽△BCA可得:BM=
,求出t值;(2)先把三角形ABC的面积求出来,过点P作PH⊥CA,垂足为点H,利用三角形相似把高PH用含有t的式子表示出来,再把三角形APQ的面积用含有t的式子表示出来,若线段PQ将△ABC的面积能分成1:2两部分,则三角形APQ的面积等于△ABC面积的三分之一,或者三分之二,建立方程求解;(3)当△CPQ为等腰三角形时,分三种情况讨论:①当PC=PQ时,过点P作PH⊥CA,垂足为点H,利用△PHA∽△BCA,建立对应边成比例求出t值;②当CP=CQ时,过点P作PM⊥CB,垂足为点M,由△BMP∽△BCA可得:BM=![]() t,MP=
t,MP=![]() t,∴CM=3-
t,∴CM=3-![]() t.在Rt△PMC 中,由勾股定理建立关于t的一元二次方程,求得t值,并讨论t值是否符合题意;③当QP=QC时,过点Q作PN⊥AB,垂足为点N,由△AQN∽△ABC可得:NQ=
t.在Rt△PMC 中,由勾股定理建立关于t的一元二次方程,求得t值,并讨论t值是否符合题意;③当QP=QC时,过点Q作PN⊥AB,垂足为点N,由△AQN∽△ABC可得:NQ=![]() t,NA=
t,NA=![]() t, ∴PN=5-t-
t, ∴PN=5-t-![]() t=5-
t=5-![]() t.在Rt△QNP 中,由勾股定理建立关于t的一元二次方程,看是否存在t值且符合题意.
t.在Rt△QNP 中,由勾股定理建立关于t的一元二次方程,看是否存在t值且符合题意.
试题解析:(1)先由勾股定理算得AB=5,分两种情况讨论:①如图1,
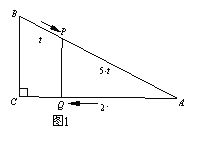
当△PQA∽△BCA时,∠PQA=∠C=90,PQ∥BC,AB=5,PB=t,PA=5-t,AQ=2t,利用相似三角形对应边成比例,即![]() ,有
,有 ![]() =
=![]() , ∴ t=
, ∴ t=![]() ;②如图2,
;②如图2,

当∠QPA=∠C=90时,△PQA∽△CBA,由题意得:PA=5-t,AQ=2t,利用相似三角形对应边成比例,即![]() ,有
,有![]() =
=![]() ,∴t=
,∴t=![]() .又∵0<t<2,∴t=
.又∵0<t<2,∴t=![]() 或
或![]() 都符合题意,所以当t=
都符合题意,所以当t=![]() 或
或![]() 时,以P、Q、A为顶点的三角形与△ABC相似.(2)过点P作PH⊥CA,垂足为点H,如图3:
时,以P、Q、A为顶点的三角形与△ABC相似.(2)过点P作PH⊥CA,垂足为点H,如图3:
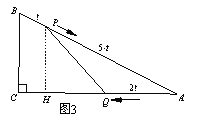
则有△PHA∽△BCA, 对应边成比例:即 ![]() =
=![]() ,∴PH=
,∴PH=![]() (5-t).∴S△APQ=
(5-t).∴S△APQ=![]() ×2t×
×2t×![]() (5-t)=-
(5-t)=-![]() t2+3t.而S△ABC=3×4÷2=6,若线段PQ将△ABC的面积分成1:2两部分,则S△APQ=
t2+3t.而S△ABC=3×4÷2=6,若线段PQ将△ABC的面积分成1:2两部分,则S△APQ=![]() S△ABC=
S△ABC=![]() ×6=2或S△APQ=
×6=2或S△APQ=![]() S△ABC=
S△ABC=![]() ×6=4,即:-
×6=4,即:-![]() t2+3t=2或-
t2+3t=2或-![]() t2+3t=4.①当-
t2+3t=4.①当-![]() t2+3t=2时,整理得:3t2-15t+10=0,t 1=
t2+3t=2时,整理得:3t2-15t+10=0,t 1=![]() (t 1=
(t 1=![]() >2)(不合题意舍去),t 2=
>2)(不合题意舍去),t 2=![]() ,∴t=
,∴t=![]() 时线段PQ将△ABC的面积分成1:2两部分;②当-
时线段PQ将△ABC的面积分成1:2两部分;②当-![]() t2+3t=4时,整理得:3t2-15t+20=0,∵△<0,∴t无解.综上所述t=
t2+3t=4时,整理得:3t2-15t+20=0,∵△<0,∴t无解.综上所述t=![]() 时线段PQ将△ABC的面积分成1:2两部分;
时线段PQ将△ABC的面积分成1:2两部分;
(3)若△CPQ为等腰三角形,则分三种情况讨论:①如图4,
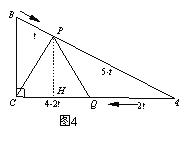
当PC=PQ时,过点P作PH⊥CA,垂足为点H,由三线合一可知:HQ=(4-2t)÷2=2-t,又△PHA∽△BCA,所以![]() ,即
,即 ![]() =
=![]() ,解得:t=
,解得:t=![]() ;②如图5,
;②如图5,
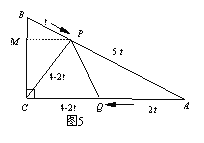
当CP=CQ时,过点P作PM⊥CB,垂足为点M,由△BMP∽△BCA可知:![]() ,即BM=
,即BM=![]() t,
t,![]() ,即MP=
,即MP=![]() t,∴CM=3-
t,∴CM=3-![]() t.在Rt△PMC中,PC=CQ=4-2t,由勾股定理得:(
t.在Rt△PMC中,PC=CQ=4-2t,由勾股定理得:(![]() t)2+(3-
t)2+(3-![]() t)2=(4-2t)2,整理得:15t2-62t+35=0,∴t=
t)2=(4-2t)2,整理得:15t2-62t+35=0,∴t=![]() ,即t1=
,即t1=![]() ,t 2=
,t 2=![]() ,∵t 1=
,∵t 1=![]() >2.∴t 1=
>2.∴t 1=![]() (舍去),∴t=
(舍去),∴t=![]() .③如图6,
.③如图6,

当QP=QC=4-2t时,过点Q作PN⊥AB,垂足为点N,由△AQN∽△ABC可知:NQ=![]() t,NA=
t,NA=![]() t, ∴PN=5-t-
t, ∴PN=5-t-![]() t=5-
t=5-![]() t.在Rt△QNP 中,由勾股定理得:(
t.在Rt△QNP 中,由勾股定理得:(![]() t)2+(5-
t)2+(5-![]() t)2=(4-2t)2 ,整理得:21t2-50t+45=0,∵△=-1280<0 ,∴t无解.综上所述当t=
t)2=(4-2t)2 ,整理得:21t2-50t+45=0,∵△=-1280<0 ,∴t无解.综上所述当t=![]() 或t=
或t=![]() 时,△CPQ是等腰三角形.
时,△CPQ是等腰三角形.

 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案






