题目内容
【题目】已知直线![]() 交
交![]() 轴于
轴于![]() 点,交
点,交![]() 轴于
轴于![]() 点,
点, ![]() 为
为![]() 的中点,
的中点, ![]() 为射线
为射线![]() 上一点,连
上一点,连![]() ,将
,将![]() 绕
绕![]() 点顺时针旋转
点顺时针旋转![]() 得线段
得线段![]() ,则
,则![]() 的最小值为__________.
的最小值为__________.
【答案】![]()
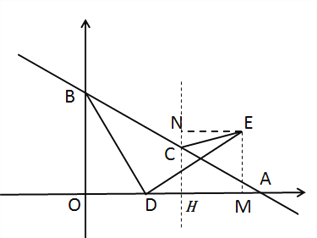
【解析】根据题意,画出图形(如图所示),直线![]() 交
交![]() 轴于
轴于![]() 点,交
点,交![]() 轴于
轴于![]() 点,
点, ![]() 为
为![]() 的 中点,可得A(4,0),B(0,2),C(2,1),所以OB=2,0A=4.过点E作EM⊥x轴于点M,过点E作NC⊥x轴,过点E作EN⊥NC于点N,因为BD⊥DE,∠BOD=∠AMD=90°,即可证得∠ODB=∠MED,再由BD=DE,根据AAS即可判定△ODB≌△MED,根据全等三角形的对应边相等可得OD=EM,OB=DM=2,设OD=EM=m,则OM=2+m,由点C为AB的中点可得OH=HM=2,即可求得HM=m,所以EN=m.又因C(2,1),EM=NH=m,可得NC=m-1.在Rt△CNE中,根据勾股定理可得
的 中点,可得A(4,0),B(0,2),C(2,1),所以OB=2,0A=4.过点E作EM⊥x轴于点M,过点E作NC⊥x轴,过点E作EN⊥NC于点N,因为BD⊥DE,∠BOD=∠AMD=90°,即可证得∠ODB=∠MED,再由BD=DE,根据AAS即可判定△ODB≌△MED,根据全等三角形的对应边相等可得OD=EM,OB=DM=2,设OD=EM=m,则OM=2+m,由点C为AB的中点可得OH=HM=2,即可求得HM=m,所以EN=m.又因C(2,1),EM=NH=m,可得NC=m-1.在Rt△CNE中,根据勾股定理可得![]() ,当
,当![]() 时,
时, ![]() 最小,最小为
最小,最小为![]() ,所以EC最小为
,所以EC最小为![]() .
.

 阅读快车系列答案
阅读快车系列答案【题目】目前节能灯在城市已基本普及,为响应号召,某商场计划购进甲,乙两种节能灯共200只,这两种节能灯的进价、售价如下表:
进价(元/只) | 售价(元/只) | |
甲型 | 20 | 30 |
乙型 | 30 | 45 |
(1)若购进甲,乙两种节能灯共用去5200元,求甲、乙两种节能灯各进多少只?
(2)若商场准备用不多于5400元购进这两种节能灯,问甲型号的节能灯至少进多少只?
(3)在(2)的条件下,该商场销售完200只节能灯后能否实现盈利超过2690元的目标?若能请你给出相应的采购方案;若不能说明理由.
【题目】体育课上,七年级某班男同学进行了100米测验,达标成绩为15秒,下表是梦想小组8名男生的成绩记录,其中“+”表示成绩大于15秒.
﹣0.8 | +1 | ﹣1.2 | 0 | ﹣0.7 | +0.6 | ﹣0.4 | ﹣0.1 |
问:(1)这个小组男生的达标率为多少?(达标率=![]() )
)
(2)这个小组男生的平均成绩是多少秒?