题目内容
【题目】用大小相等的小正方形(阴影部分)按一定规律拼成下列图形,拼成第1个图形需要2个小正方形,拼第2个图形需要6个小正方形,拼第3个图形需要12个小正方形……那么第5个图形中需要小正方形个, 第n个图形中需要小正方形个.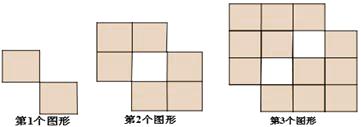
【答案】30;n(n+1)
【解析】解:拼成第1个图形需要1![]() 2=2个小正方形;
2=2个小正方形;
拼成第2个图形需要2![]() 3=6个小正方形;
3=6个小正方形;
拼成第3个图形需要3![]() 4=12个小正方形;
4=12个小正方形;
拼成第4个图形需要4![]() 5=20个小正方形;
5=20个小正方形;
拼成第5个图形需要5![]() 6=30个小正方形;
6=30个小正方形;
......
拼成第n个图形需要n(n+1)个小正方形.
所以答案是:30;n(n+1).
【考点精析】关于本题考查的数与式的规律,需要了解先从图形上寻找规律,然后验证规律,应用规律,即数形结合寻找规律才能得出正确答案.

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目
【题目】如图所示的日历中,任意圈出一竖列相邻的三个数,设中间一个数为a,则这三个数之和为(用含a的式子表示)
日 | 一 | 二 | 三 | 四 | 五 | 六 |
1 | 2 | 3 | 4 | |||
5 | 6 | 7 | 8 | 9 | 10 | 11 |
12 | 13 | 14 | 15 | 16 | 17 | 18 |
19 | 20 | 21 | 22 | 23 | 24 | 25 |
26 | 27 | 28 | 29 | 30 | 31 |