题目内容
a、b都是有理数,下面给出4个判断,其中正确的判断只有( )
⑴若a+b<a,则b<0 ⑵若ab<a则b<0 ⑶若a-b<a, 则b>0 ⑷若a>b,则b>0
⑴若a+b<a,则b<0 ⑵若ab<a则b<0 ⑶若a-b<a, 则b>0 ⑷若a>b,则b>0
| A.⑴⑵ | B.⑵⑶ | C.⑴⑶ | D.⑴⑷ |
C
分析:①利用不等式性质1,同减去a,不等号不变,故正确;②若a<0,利用不等式性质3,同除以a,不等号改变,故错误;③先利用不等式性质1,同减去a,方向不变,再利用不等式性质3,同乘以-1,方向改变,故正确;④若b<0,利用不等式性质3,同除以b,不等号方向改变,故错误.
解答:解:①∵a+b<a,
∴b<0(不等式性质1),
故此选项正确;
②∵ab<a,
若a<0,
∴b>0(不等式性质3),
故此选项错误;
③∵a-b<a,
∴-b<0(不等式性质1),
∴b>0(不等式性质3),
故此选项正确;
④∵a>b,b可正可负,故此选项错误.
故正确的是①③.
故选C.
点评:不等式的性质:(1)不等式两边加(或减)同一个数(或式子),不等号的方向不变.
(2)不等式两边乘(或除以)同一个正数,不等号的方向不变.
(3)不等式两边乘(或除以)同一个负数,不等号的方向改变.
解答:解:①∵a+b<a,
∴b<0(不等式性质1),
故此选项正确;
②∵ab<a,
若a<0,
∴b>0(不等式性质3),
故此选项错误;
③∵a-b<a,
∴-b<0(不等式性质1),
∴b>0(不等式性质3),
故此选项正确;
④∵a>b,b可正可负,故此选项错误.
故正确的是①③.
故选C.
点评:不等式的性质:(1)不等式两边加(或减)同一个数(或式子),不等号的方向不变.
(2)不等式两边乘(或除以)同一个正数,不等号的方向不变.
(3)不等式两边乘(或除以)同一个负数,不等号的方向改变.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
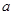 、
、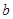 在数轴上的位置如图所示,则化简
在数轴上的位置如图所示,则化简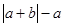 的结果为( )
的结果为( )
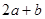
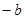

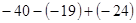
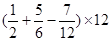
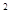 -(-2)
-(-2)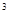 ×(-1)
×(-1)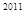

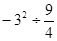 +|-4|×0.5
+|-4|×0.5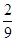 ×(-1
×(-1 )
)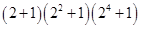 的结果为 .
的结果为 . 。
。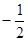 的相反数是( )
的相反数是( )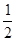
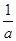 -
-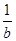 ( ab ≠ 0 ),则3*5 =
( ab ≠ 0 ),则3*5 = 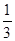 -
-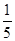 =
= 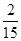 ,
,