题目内容
【题目】已知△ABC是等边三角形,点D为平面内一点,连接DB、DC,∠BDC=120°.
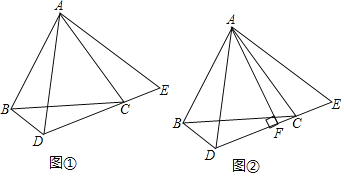
(1)如图①,当点D在BC下方时,连接AD,延长DC到点E,使CE=BD,连接AE.
①求证:△ABD≌△ACE;
②如图②,过点A作AF⊥DE于点F,直接写出线段AF、BD、DC间的数量关系;
(2)若AB=2![]() ,DC=6,直接写出点A到直线BD的距离.
,DC=6,直接写出点A到直线BD的距离.
【答案】(1)①证明见解析;②AF=![]() (CD+BD);(2)4
(CD+BD);(2)4![]() 或
或![]()
【解析】
(1)①由等边三角形的性质可得AB=AC=BC,∠ABC=∠ACB=∠BAC=60°,由四边形的内角和定理可得∠ACE=∠ABD,由“SAS”可证△ABD≌△ACE;
②由全等三角形的性质可得AD=AE,∠BAD=∠CAE,可证△ADE是等边三角形,可得AF=![]() DF=
DF=![]() AD,即可求解;
AD,即可求解;
(2)分两种情况讨论,当点D在BC下方时,利用全等三角形的性质和勾股定理可求点A到直线BD的距离;当点D在BC上方时,过点C作CH⊥BD交BD延长线于H,过点D作DF⊥BC于F,过点A作AN⊥BD,交BD的延长线于N,利用面积法可求DF的长,由三角函数可求解.
证明:(1)①∵△ABC是等边三角形,
∴AB=AC=BC,∠ABC=∠ACB=∠BAC=60°,
∵∠ABD+∠BDC+∠ACD+∠BAC=360°,∠BDC=120°,
∴∠ABD+∠ACD=180°,
∵∠ACE+∠ACD=180°,
∴∠ACE=∠ABD,
又∵AB=AC,BD=CE,
∴△ABD≌△ACE(SAS);
②∵△ABD≌△ACE,
∴AD=AE,∠BAD=∠CAE,
∴∠DAC+∠CAE=∠DAC+∠BAD=∠BAC=60°,
∴∠DAE=60°,
∴△ADE是等边三角形,
∴AD=ED,
∵AF⊥DE,AD=AE,
∴DF=![]() DE=
DE=![]() AD,∠DAF=30°,
AD,∠DAF=30°,
∴AF=![]() DF=
DF=![]() AD,
AD,
∵DE=CD+CE=CD+BD,
∴AF=![]() AD=
AD=![]() (CD+BD);
(CD+BD);
(2)如图②,若点D在BC下方时,
∵△ABD≌△ACE,
∴点A到直线BD的距离=点A到直线CE的距离,
设DF=x,则AF=![]() x,
x,
∵AC2=AF2+CF2,
∴52=3x2+(6﹣x)2,
∴x1=4,x2=﹣1(舍去),
∴AF=4![]() ,
,
如图3,若点D在BC上方时,过点C作CH⊥BD交BD延长线于H,过点D作DF⊥BC于F,过点A作AN⊥BD,交BD的延长线于N,
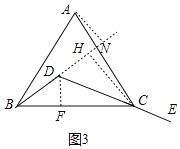
∵∠BDC=120°,
∴∠CDH=60°,
∵CH⊥BD,
∴∠DCH=30°,CD=6,
∴DH=3,CH=![]() DH=3
DH=3![]() ,
,
∵BH=![]() =
=![]() =5,
=5,
∴BD=BH﹣DH=2,
∵S△BDC=![]() BD×CH=
BD×CH=![]() ×BC×DF,
×BC×DF,
∴2×3![]() =2
=2![]() ×DF,
×DF,
∴DF=![]() ,
,
∵∠BDC=120°,
∴∠DBC+∠DCB=60°,
又∵∠ABD+∠DBC=60°,
∴∠ABD=∠DCB,
∴sin∠ABD=sin∠DCB=![]() ,
,
∴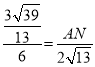 ,
,
∴AN=![]() ,
,
综上所述:点A到直线BD的距离为4![]() 或
或![]() .
.