题目内容
(2004•厦门)已知圆心在原点,半径为1的⊙O,直线AB与⊙O切于点P (m,n).且与x、y轴交于点A(a,0)、B(0,b)(a>0,b>0).(1)如图1,当m=
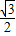 时,求a的值;
时,求a的值;(2)如图2,连接OP,过P向x轴引垂线交x轴于点C,设x表示△OPC的面积,y=a+b,试求y与x之间的函数关系式,并写出自变量x的取值范围.
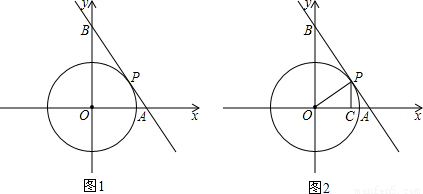
【答案】分析:(1)过P作PC⊥x轴于C,在直角三角形OPA中,根据射影定理可得出OP2=OC•OA,即a= ,同理可得出b=
,同理可得出b=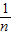 ,据此可根据m的值求出a的值;
,据此可根据m的值求出a的值;
(2)根据(1)的结果,可用m,n替换掉y=a+b中的a和b.然后根据mn=x,m2+n2=1即可得出y与x的函数关系式.
解答:解:(1)过P作PC⊥OA于C,
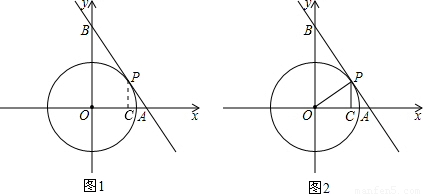
∵AB是圆O的切线,因此OP⊥AB,
根据射影定理可得:OP2=OC•OA,即a=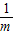 ,同理可得b=
,同理可得b=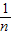 ,
,
因此当m=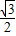 时,a=
时,a=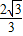 ;
;
(2)根据题意可知:OP=1,因此m2+n2=1,
而△OCP的面积为x,即 mn=x,mn=2x,
mn=x,mn=2x,
∴y=a+b=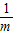 +
+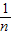 =
=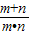 =
=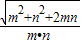 =
=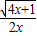
∵当PC=CO时,x最大,此时OP=1,得出PC=CO=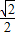 ,
,
∴x= ×
×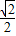 ×
×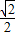 =
= ,
,
∴0<x≤ .
.
点评:主要考查了函数和几何图形的综合运用.
 ,同理可得出b=
,同理可得出b=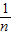 ,据此可根据m的值求出a的值;
,据此可根据m的值求出a的值;(2)根据(1)的结果,可用m,n替换掉y=a+b中的a和b.然后根据mn=x,m2+n2=1即可得出y与x的函数关系式.
解答:解:(1)过P作PC⊥OA于C,

∵AB是圆O的切线,因此OP⊥AB,
根据射影定理可得:OP2=OC•OA,即a=
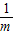 ,同理可得b=
,同理可得b=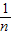 ,
,因此当m=
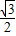 时,a=
时,a=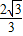 ;
;(2)根据题意可知:OP=1,因此m2+n2=1,
而△OCP的面积为x,即
 mn=x,mn=2x,
mn=x,mn=2x,∴y=a+b=
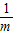 +
+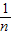 =
=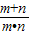 =
=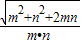 =
=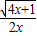
∵当PC=CO时,x最大,此时OP=1,得出PC=CO=
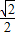 ,
,∴x=
 ×
×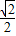 ×
×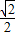 =
= ,
,∴0<x≤
 .
.点评:主要考查了函数和几何图形的综合运用.

练习册系列答案
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案
相关题目