题目内容
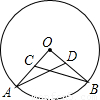
(2004•厦门)已知:如图,OA、OB为⊙O的半径,C、D分别为OA、OB的中点,若AD=3厘米,则BC= 厘米.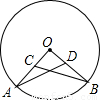
【答案】分析:首先证明△AOD≌△BOC,然后利用它们对应边相等就可以得到BC的长度.
解答:解:∵OA、OB为⊙O的半径
∴OA=OB
∵C、D分别为OA、OB的中点
∴OD=OC,∠AOD公共角
∴△AOD≌△BOC
∴BC=AD=3厘米.
点评:本题考查了全等三角形的判定及全等三角形性质的应用,确认两条线段或两个角相等,往往利用全等三角形的性质求解.
解答:解:∵OA、OB为⊙O的半径
∴OA=OB
∵C、D分别为OA、OB的中点
∴OD=OC,∠AOD公共角
∴△AOD≌△BOC
∴BC=AD=3厘米.
点评:本题考查了全等三角形的判定及全等三角形性质的应用,确认两条线段或两个角相等,往往利用全等三角形的性质求解.

练习册系列答案
相关题目