题目内容
【题目】如图，矩形ABCD绕点B逆时针旋转30°后得到矩形A1BC1D1，C1D1与AD交于点M，延长DA交A1D1于F，若AB=1，BC=
，则AF的长度为（ ）
A．
B．
C．
D．
【答案】A．
【解析】
试题分析：连接BD，如图所示：
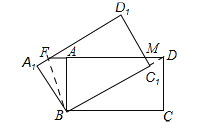
在矩形ABCD中，∠C=90°，CD=AB=1，在Rt△BCD中，CD=1，BC=
，∴tan∠CBD=
，BD=2，∴∠CBD=30°，∠ABD=60°，由旋转得，∠CBC1=∠ABA1=30°，∴点C1在BD上，连接BF，由旋转得，AB=A1B，∵矩形A1BC1D1是矩形ABCD旋转所得，∴∠BA1F=∠BAF=90°，∵AF=AF，∴△A1BF≌△ABF，∴∠A1BF=∠ABF，∵∠ABA1=30°，∴∠ABF=
∠ABA1=15°，∵∠ABD=60°，∴∠DBF=75°，∵AD∥BC，∴∠ADB=∠CBD=30°，∴∠BFD=75°，∴DF=BD=2，∴AF=DF﹣AD=
，故选A．
练习册系列答案
相关题目
