题目内容
【题目】如图,在ABC中,∠A=∠B=30°,过点C作CD⊥AC,交AB于点D.

(1)作△ACD外接圆⊙O(尺规作图,保留作图痕迹,不写作法);
(2)判断直线BC与⊙O的位置关系,并证明你的结论.
【答案】(1)见解析;(2)BC与⊙O相切.
【解析】
试题分析:(1)先作线段AD的垂直平分线交AD于O点,然后以O为圆心,OA为半径画圆即可;
(2)连接CO,如图,利用三角形外角性质得到∠COB=2∠A=60°,则∠COB+∠B=90°,所以∠OCB=90°,然后根据切线的判定定理可判断BC与⊙O相切.
解:(1)如图,⊙O为所作;
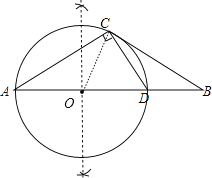
(2)BC与⊙O相切.
证明如下:连接CO,如图,
∵∠A=∠B=30°,
∴∠COB=2∠A=60°,
∴∠COB+∠B=30°+60°=90°,
∴∠OCB=90°,
∴OC⊥BC,
又BC经过半径OC的外端点C,
∴BC与⊙O相切.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目