题目内容
已知二次函数的图象交x轴于A、B两点,对称轴方程为x=2,若AB=6,且此二次函数的最大值为5,则此二次函数的解析式为________.
y=- x2+
x2+ x+
x+ .
.
分析:先设出二次函数的解析式,因知道对称轴x=2及二次函数的最大值为5,可设函数解析式为:y=a(x-2)2+5,再根据二次函数的图象交x轴于A、B两点且AB=6,知方程a(x-2)2+5=0的两根x1,x2有|x1-x2|=6,代入可以求出a值,从而求出二次函数的解析式.
解答:设函数的解析式为:y=a(x-2)2+5,
设方程a(x-2)2+5=ax2-4ax+4a+5=0的两根为:x1,x2
二次函数的图象交x轴于A、B两点,且AB=6,
∴|x1-x2|=6,
∵x1+x2=4,x1•x2=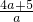 ,
,
∴|x1-x2|=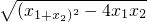 =6,
=6,
∴16-4×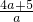 =36,
=36,
解得a=- ,
,
∴此二次函数的解析式为:y=- x2+
x2+ x+
x+ .
.
点评:此题考查一次函数的基本性质,知道对称轴和函数最大值把二次函数设为顶点式,学会用待定系数法求出二次函数的解析式,还考查学生的计算能力.
 x2+
x2+ x+
x+ .
.分析:先设出二次函数的解析式,因知道对称轴x=2及二次函数的最大值为5,可设函数解析式为:y=a(x-2)2+5,再根据二次函数的图象交x轴于A、B两点且AB=6,知方程a(x-2)2+5=0的两根x1,x2有|x1-x2|=6,代入可以求出a值,从而求出二次函数的解析式.
解答:设函数的解析式为:y=a(x-2)2+5,
设方程a(x-2)2+5=ax2-4ax+4a+5=0的两根为:x1,x2
二次函数的图象交x轴于A、B两点,且AB=6,
∴|x1-x2|=6,
∵x1+x2=4,x1•x2=
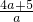 ,
,∴|x1-x2|=
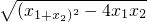 =6,
=6,∴16-4×
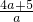 =36,
=36,解得a=-
 ,
,∴此二次函数的解析式为:y=-
 x2+
x2+ x+
x+ .
.点评:此题考查一次函数的基本性质,知道对称轴和函数最大值把二次函数设为顶点式,学会用待定系数法求出二次函数的解析式,还考查学生的计算能力.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目