题目内容
【题目】如图，△ABC的中线AE，BD交于点G，过点D作DM∥BC交AE于点M，则△AMD，△DMG和△BEG的面积之比为 ． 
【答案】3：1：4
【解析】解：∵线段AE、BD是△ABC的中线，
∴BE=CE，AD=CD，
∵DM∥BC，
∴AM=ME，
∴DM= 
CE= BE，
∵DM∥BC，
∴△DMG∽△BEG，
∴ 
= ，S△BGE：S△DMG=4：1，
∴AM：MG=3：1，
∴S△ADM：S△DMG=3：1，
∴S△AMD=3S△DMG ，
∴△AMD，△DMG和△BEG的面积之比为：3：1：4．
所以答案是：3：1：4．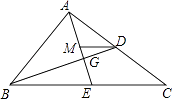
【考点精析】关于本题考查的相似三角形的判定与性质，需要了解相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等）的比等于相似比；相似三角形周长的比等于相似比；相似三角形面积的比等于相似比的平方才能得出正确答案．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
