题目内容
(2012•朝阳一模)如图,等腰△ABC中,AB=BC=5cm,AC=3cm,将△ABC绕点A按顺时针旋转至△AB′C′,使点C′恰好落在边BC上.则BC′的长是 cm.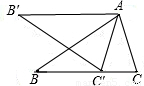
【答案】分析:根据旋转的性质,对应点到旋转中心的距离相等,即AC=AC′,△ACC′为等腰三角形,又△BCA为等腰三角形,公共底角∠C,可证△ACC′∽△BCA,利用对应边的比相等求CC′,从而可求BC′.
解答:解:由旋转可知,AC=AC′,
又AB=BC,∠ACC′=∠BCA,
∴△ACC′∽△BCA,
∴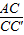 =
=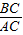 ,即
,即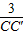 =
= ,
,
解得CC′=1.8,
BC′=BC-CC′=5-1.8=3.2cm.
点评:本题考查了旋转的性质,等腰三角形相似的判定及性质的运用.
解答:解:由旋转可知,AC=AC′,
又AB=BC,∠ACC′=∠BCA,
∴△ACC′∽△BCA,
∴
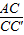 =
=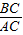 ,即
,即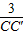 =
= ,
,解得CC′=1.8,
BC′=BC-CC′=5-1.8=3.2cm.
点评:本题考查了旋转的性质,等腰三角形相似的判定及性质的运用.

练习册系列答案
相关题目
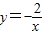 ,x与y的对应值如下表:
,x与y的对应值如下表: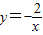


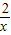 的解为 .
的解为 .