题目内容
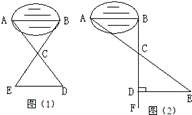
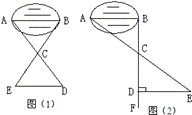
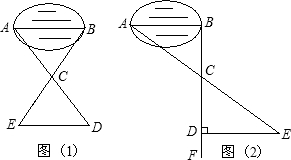
某班同学到野外活动,为测量一池塘两端A、B的距离,设计了几种方案,下面介绍两种:(I)如图(1),先在平地取一个可以直接到达A、B的点C,并分别延长AC到D,BC到E,使DC=AC,BC=EC,最后测出DE的距离即为AB的长.
(II)如图(2),先过B点作AB的垂线BF,再在BF上取C、D两点,使BC=CD,接着过点D作BD的垂线DE,交AC的延长线于E,则测出DE的长即为AB的距离.
阅读后回答下列问题:
(1)方案(I)是否可行?
(2)方案(II)是否切实可行?
(3)方案(II)中作BF⊥AB,ED⊥BF的目的是
(4)方案(II)中,若使BC=n•CD,能否测得(或求出)AB的长?理由是
分析:(1)由题意可证明△ACB≌△DCE,AB=DE,故方案(Ⅰ)可行;
(2)由题意可证明△ABC≌△EDC,AB=ED,故方案(Ⅱ)可行;
(3)方案(Ⅱ)中作BF⊥AB,ED⊥BF的目的是作直角三角形;由题意可证明△ABC∽△EDC,
=
,故此时方案(Ⅱ)成立.
(4)根据相似三角形的判定与性质得出△ABC∽△EDC,得出
=
进而求出即可.
(2)由题意可证明△ABC≌△EDC,AB=ED,故方案(Ⅱ)可行;
(3)方案(Ⅱ)中作BF⊥AB,ED⊥BF的目的是作直角三角形;由题意可证明△ABC∽△EDC,
| AB |
| ED |
| BC |
| CD |
(4)根据相似三角形的判定与性质得出△ABC∽△EDC,得出
| AB |
| ED |
| BC |
| CD |
解答:解:(1)方案(Ⅰ)可行;
∵DC=AC,EC=BC且有对顶角∠ACB=∠DCE,
∴△ACB≌△DCE(SAS),
∴AB=DE,
∴测出DE的距离即为AB的长.
故方案(Ⅰ)可行.
(2)方案(Ⅱ)可行;
∵AB⊥BC,DE⊥CD,
∴∠ABC=∠EDC=90°,
又∵BC=CD,∠ACB=∠ECD,
∴△ABC≌△EDC,
∴AB=ED,
∴测出DE的长即为AB的距离.
故方案(Ⅱ)可行.
(3)方案(Ⅱ)中作BF⊥AB,ED⊥BF的目的是作直角三角形;
若∠ABD=∠BDE≠90°,∠ACB=∠ECD,
∴△ABC∽△EDC,
∴
=
,
∴只要测出ED、BC、CD的长,即可求得AB的长.
∵BC=CD,∴ED=AB,
∴方案(Ⅱ)成立.
(4)根据(3)中所求可以得出,
∴
=
,
∵BC=n•CD,
∴
=n,求出DE即可得出答案,
当ED=m,则AB=mn.
∵DC=AC,EC=BC且有对顶角∠ACB=∠DCE,
∴△ACB≌△DCE(SAS),
∴AB=DE,
∴测出DE的距离即为AB的长.
故方案(Ⅰ)可行.
(2)方案(Ⅱ)可行;
∵AB⊥BC,DE⊥CD,
∴∠ABC=∠EDC=90°,
又∵BC=CD,∠ACB=∠ECD,
∴△ABC≌△EDC,
∴AB=ED,
∴测出DE的长即为AB的距离.
故方案(Ⅱ)可行.
(3)方案(Ⅱ)中作BF⊥AB,ED⊥BF的目的是作直角三角形;
若∠ABD=∠BDE≠90°,∠ACB=∠ECD,
∴△ABC∽△EDC,
∴
| AB |
| ED |
| BC |
| CD |
∴只要测出ED、BC、CD的长,即可求得AB的长.
∵BC=CD,∴ED=AB,
∴方案(Ⅱ)成立.
(4)根据(3)中所求可以得出,
∴
| AB |
| ED |
| BC |
| CD |
∵BC=n•CD,
∴
| AB |
| ED |
当ED=m,则AB=mn.
点评:此题主要考查了全等三角形的证明及性质和相似三角形的判定和性质.熟练地应用此性质是解决问题的关键.

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目