题目内容
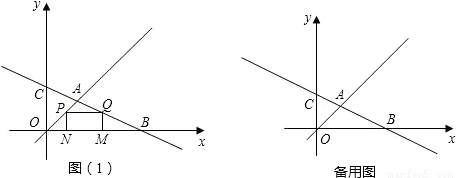
(2008•永春县)在平面直角坐标系中,直线y=- x+6与x轴、y轴分别交于B、C两点.
x+6与x轴、y轴分别交于B、C两点.(1)直接写出B、C两点的坐标;
(2)直线y=x与直线y=-
 x+6交于点A,动点P从点O沿OA方向以每秒1个单位的速度运动,设运动时间为t秒(即OP=t).过点P作PQ∥x轴交直线BC于点Q.
x+6交于点A,动点P从点O沿OA方向以每秒1个单位的速度运动,设运动时间为t秒(即OP=t).过点P作PQ∥x轴交直线BC于点Q.①若点P在线段OA上运动时(如图1),过P、Q分别作x轴的垂线,垂足分别为N、M,设矩形PQMN的面积为S,写出S和t之间的函数关系式,并求出S的最大值.
②若点P经过点A后继续按原方向、原速度运动,当运动时间t为何值时,过P、Q、O三点的圆与x轴相切?
【答案】分析:(1)令x=0以及y=0代入题中相应的函数关系式可求出B,C的坐标.
(2)已知点P在y=x上,OP=t,可求出点P,Q的坐标以及PQ的长.然后根据矩形公式求出S关于t的函数关系式化简求出S的最大值.
根据题意,点P经过A点后继续按原方向,原速度运动,则圆心在y轴上且y轴垂直平分PQ.得出∠POC=∠QOC=45°.
解答:解:(1)令x=0,则y=6;令y=0,则x=12,
∴B(12,0),C(0,6).
(2)①点P在y=x上,OP=t,点P坐标(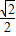 t,
t,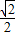 t),点Q坐标(12-
t),点Q坐标(12-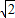 t,
t,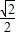 t).
t).
PQ=12-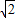 t-
t-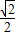 t=12-
t=12-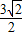 t,PN=
t,PN= t.
t.
S=PQ•PN=-1.5t2+6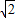 t=-1.5(t2-4
t=-1.5(t2-4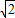 t+8)+12=-1.5(t-
t+8)+12=-1.5(t-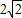 )2+12.
)2+12.
当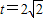 时,S的最大值为12.
时,S的最大值为12.
②若点P经过点A后继续按原方向、原速度运动,过P、Q、O三点的圆与x轴相切,
则圆心在y轴上,且y轴垂直平分PQ.
∴∠POC=45°,
∴∠QOC=45°.
∴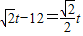 ,
,
∴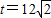 .
.
点评:本题考查的是一次函数的图象与应用,矩形的面积公式以及圆的有关知识,难度中上.
(2)已知点P在y=x上,OP=t,可求出点P,Q的坐标以及PQ的长.然后根据矩形公式求出S关于t的函数关系式化简求出S的最大值.
根据题意,点P经过A点后继续按原方向,原速度运动,则圆心在y轴上且y轴垂直平分PQ.得出∠POC=∠QOC=45°.
解答:解:(1)令x=0,则y=6;令y=0,则x=12,
∴B(12,0),C(0,6).

(2)①点P在y=x上,OP=t,点P坐标(
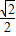 t,
t,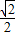 t),点Q坐标(12-
t),点Q坐标(12-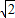 t,
t,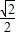 t).
t).PQ=12-
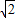 t-
t-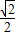 t=12-
t=12-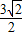 t,PN=
t,PN= t.
t.S=PQ•PN=-1.5t2+6
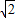 t=-1.5(t2-4
t=-1.5(t2-4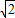 t+8)+12=-1.5(t-
t+8)+12=-1.5(t-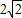 )2+12.
)2+12.当
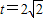 时,S的最大值为12.
时,S的最大值为12.②若点P经过点A后继续按原方向、原速度运动,过P、Q、O三点的圆与x轴相切,
则圆心在y轴上,且y轴垂直平分PQ.
∴∠POC=45°,
∴∠QOC=45°.
∴
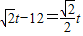 ,
,∴
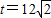 .
.点评:本题考查的是一次函数的图象与应用,矩形的面积公式以及圆的有关知识,难度中上.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
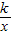 的图象经过点(1,6),则k等于 .
的图象经过点(1,6),则k等于 .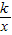 的图象经过点(1,6),则k等于 .
的图象经过点(1,6),则k等于 .