Question

（2013•徐州模拟）如图所示，甲、乙两船同时由港口A出发开往海岛B，甲船沿东北方向向海岛B航行，其速度为15海里/小时；乙船速度为20海里/小时，先沿正东方向航行1小时后，到达C港口接旅客，停留半小时后再转向北偏东30°方向开往B岛，其速度仍为20海里/小时．
（1）求港口A到海岛B的距离；
（2）B岛建有一座灯塔，在离灯塔方圆5海里内都可以看见灯塔，问甲、乙两船哪一艘先看到灯塔？

Answer 1

分析：（1）作BD⊥AE于D，构造两个直角三角形并用解直角三角形用BD表示出CD和AD，利用DA和DC之间的关系列出方程求解．
（2）分别求得两船看见灯塔的时间，然后比较即可．

解答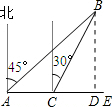：解：（1）过点B作BD⊥AE于D
在Rt△BCD中，∠BCD=60°，设CD=x，则BD=

3

x，BC=2x
在Rt△ABD中，∠BAD=45°
则AD=BD=

3

x，AB=

2

BD=

6

x
由AC+CD=AD得20+x=

3

x
解得：x=10

3

+10
故AB=30

2

+10

6

答：港口A到海岛B的距离为30

2

+10

6

海里．

（2）甲船看见灯塔所用时间：

30 2 +10 6 -5

15

≈4.1小时
乙船看见灯塔所用时间：1+

1

2

+

20 3 +20-5

20

≈4.0小时
所以乙船先看见灯塔．

点评：此题考查的知识点是勾股定理的应用，解答此类题目的关键是构造出直角三角形，利用解直角三角形的相关知识解答．