题目内容
若a＜0，ab＜0，则|b-a+3|-|a-b-9|的值为
- A.6
- B.-6
- C.12
- D.-2a+2b+12
B
分析：根据所给题意，可判断出a，b的正负性，然后再根据绝对值的定义，去掉绝对值，化简求解．
解答：∵a＜0，ab＜0，
∴a＜0，b＞0，
∴b-a＞0，a-b＜0
∴b-a+3＞0，a-b-9＜0，
∴|b-a+3|-|a-b-9|=b-a+3+（a-b-9）=-6．
故本题的答案选B．
点评：主要考查绝对值性质的运用．解此类题的关键是：先利用条件判断出绝对值符号里代数式的正负性，再根据绝对值的性质把绝对值符号去掉，把式子化简，即可求解．
分析：根据所给题意，可判断出a，b的正负性，然后再根据绝对值的定义，去掉绝对值，化简求解．
解答：∵a＜0，ab＜0，
∴a＜0，b＞0，
∴b-a＞0，a-b＜0
∴b-a+3＞0，a-b-9＜0，
∴|b-a+3|-|a-b-9|=b-a+3+（a-b-9）=-6．
故本题的答案选B．
点评：主要考查绝对值性质的运用．解此类题的关键是：先利用条件判断出绝对值符号里代数式的正负性，再根据绝对值的性质把绝对值符号去掉，把式子化简，即可求解．
练习册系列答案
课时掌控随堂练习系列答案
一课一练一本通系列答案
浙江之星学业水平测试系列答案
相关题目
10、如图所示，以下四种结论：①若∠1=∠2，则AB∥CD；②若∠1=∠2，则AD∥BC；③若∠3=∠4，则AB∥CD；④若∠3=∠4，则AD∥BC，其中正确的是（ ）
（2013•重庆）如图，在矩形ABCD中，E、F分别是边AB、CD上的点，AE=CF，连接EF、BF，EF与对角线AC交于点O，且BE=BF，∠BEF=2∠BAC．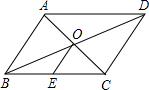
平行四边形ABCD中，对角线AC、BD交于点O，点E是BC的中点．若OE=3cm，则AB的长为（ ）