题目内容
【题目】解方程组:
(1) ![]() (2)
(2) 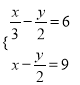
(3) 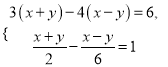 (4)
(4) 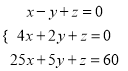
【答案】(1) ![]() (2)
(2)  (3)
(3) ![]() (4)
(4) 
【解析】试题分析:(1)根据方程的特点,利用代入消元法求解即可;
(2)根据方程的特点,利用加减消元法求解即可;
(3)把x+y和x-y看做一个整体,然后利用加减消元法求解即可;
(4)利用加减消元法先消去未知数z,然后解二元一次方程组即可求出三元一次方程组的解.
试题解析:(1) ![]()
由①,得x=3+2y.③
将③代入②,得9+6y+y=2,
即y=-1.
将y=-1代入③,得x=3-2=1.
所以原方程组的解为![]() .
.
(2) 
②-①,得![]() x=3,解得x=
x=3,解得x=![]() .
.
将x=![]() 代入①得
代入①得![]() =6,
=6,
解得y=-9.
所以原方程组的解为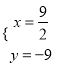
(3) 
②×6,得3(x+y)-(x-y)=6,③
①-③,得-3(x-y)=0,即x=y.
将x=y代入③,得3(x+x)-0=6,即x=1.所以y=1.
所以原方程组的解为![]()
(4) 
②-①,得3x+3y=0,④
③-①,得24x+6y=60,⑤
④⑤组成方程组得
![]() ,解得
,解得
将 代入①,得z=-
代入①,得z=-![]() .
.
所以原方程组的解为

练习册系列答案
相关题目
【题目】为了了解江城中学学生的身高情况,随机对该校男生、女生的身高进行抽样调查,已知抽取的样本中,男生、女生的人数相同,根据所得数据绘制成如下所示的统计表和如图所示的统计图.
组别 | 身高(cm) |
A | x<150 |
B | 150≤x<155 |
C | 155≤x<160 |
D | 160≤x<165 |
E | x≥165 |
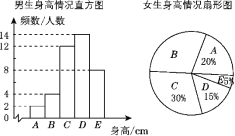
根据图表中提供的信息,回答下列问题:
(1)女生身高在B组的有________人;
(2)在样本中,身高在150≤x<155之间的共有________人,身高人数最多的在________组(填组别序号);
(3)已知该校共有男生500人,女生480人,请估计身高在155≤x<165之间的学生有多少人.