题目内容
【题目】如图1，点P、Q分别是等边△ABC边AB、BC上的动点（端点除外），点P从顶点A、点Q从顶点B同时出发，且它们的运动速度相同，连接AQ、CP交于点M．
（1）求证：△ABQ≌△CAP；
（2）当点P、Q分别在AB、BC边上运动时，∠QMC变化吗？若变化，请说明理由；若不变，求出它的度数．
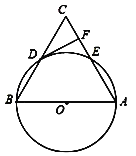
（3）如图2，若点P、Q在运动到终点后继续在射线AB、BC上运动，直线AQ、CP交点为M，则∠QMC变化吗？若变化，请说明理由；若不变，直接写出它的度数．
【答案】（1）证明见解析；（2）点P、Q在运动的过程中，∠QMC不变．理由见解析.（3）不变，理由见解析.
【解析】试题分析：(1)、根据等边三角形可得∠ABQ=∠CAP，AB=CA，根据速度相同可得AP=BQ，从而得出三角形全等；(2)、根据△ABQ≌△CAP得出∠BAQ=∠ACP，然后根据∠QMC=∠BAQ+∠MAC得出答案；(3)、根据△ABQ≌△CAP得出∠BAQ=∠ACP，然后根据∠QMC=∠BAQ+∠MAC得出答案.
试题解析：(1)、∵△ABC是等边三角形 ∴∠ABQ=∠CAP，AB=CA， 又∵点P、Q运动速度相同，
∴AP=BQ， 在△ABQ与△CAP中，AB=AC，∠ABQ=∠CAP，AP=BQ ∴△ABQ≌△CAP（SAS）；
(2)、点P、Q在运动的过程中，∠QMC不变．
理由：∵△ABQ≌△CAP， ∴∠BAQ=∠ACP， ∵∠QMC=∠ACP+∠MAC， ∴∠QMC=∠BAQ+∠MAC=∠BAC=60°
(3)、点P、Q在运动到终点后继续在射线AB、BC上运动时，∠QMC不变．
理由：∵△ABQ≌△CAP， ∴∠BAQ=∠ACP， ∵∠QMC=∠BAQ+∠APM，
∴∠QMC=∠ACP+∠APM=180°-∠PAC=180°-60°=120°
