Question

【题目】如图，△ABC的内部有一点P ， 且D、E、F是P分别以AB、BC、AC为对称轴的对称点．若△ABC的内角∠DAF＝70°，∠DBE＝60°，∠ECF＝50°，则∠ADB＋∠BEC＋∠CFA＝ ．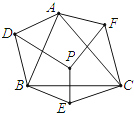

Answer 1

【答案】360°
【解析】连接AP ， BP ， CP ，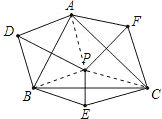

∵D ， E ， F是P分别以AB ， BC ， AC为对称轴的对称点
∴∠ADB＝∠APB ， ∠BEC＝∠BPC ， ∠CFA＝∠APC ，
∴∠ADB＋∠BEC＋∠CFA＝∠APB＋∠BPC＋∠APC＝360°．
所以答案是：360°．
【考点精析】利用轴对称的性质对题目进行判断即可得到答案，需要熟知关于某条直线对称的两个图形是全等形；如果两个图形关于某直线对称，那么对称轴是对应点连线的垂直平分线；两个图形关于某直线对称，如果它们的对应线段或延长线相交，那么交点在对称轴上．